题目内容
已知函数f（x）=
（n∈N*），试求：（1）f（x）的定义域并画出f（x）的图象；
（2）
f（x），
f（x），
f（x）；
（3）f（x）在哪些点处不连续.
解：（1）当|x|＜1，即－1＜x＜1时，=0，
当x=－1时，不存在，
当x=1时，=
，
当|x|＞1，即x＞1或x＜－1时，
=
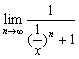=1.
∴f（x）=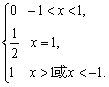
∴定义域为（－∞，－1）∪［1，+∞）.图象如下图.
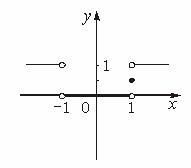
（2）
f（x）=
1=1，
f（x）=
0=0，
f（x）不存在.
（3）f（x）在x=－1及x=1处不连续.
∵f（x）在x=－1处无意义，
x=1时，
f（x）=1，
f（x）=0，
即
f（x）不存在，
∴f（x）在x=－1及x=1处不连续.
点评：求f（x）的定义域就是确定x取哪些值时f（x）有意义，即
存在.
练习册系列答案
黄冈创优卷系列答案
相关题目
已知函数f（x）=x2-bx的图象在点A（1，f（1））处的切线l与直线3x-y+2=0平行，若数列{
}的前n项和为Sn，则S2010的值为（ ）
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|