Question

设集合M=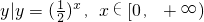，N={y|y=log₂x，x∈（0，1]}，则集合M∪N是

1. A.
   （-∞，0）∪[1，+∞）
2. B.
   [0，+∞）
3. C.
   （-∞，1]
4. D.
   （-∞，0）∪（0，1]

Answer 1

C
分析：根据指数函数性质和图象可知M中y的取值范围，根据对数函数性质和图象可知N中y的取值范围，然后让两者取并集即可．
解答：根据指数函数图象和性质M中y在【0，+∞）上的取值范围为（0，1】，
根据对数函数的图象和性质N中y在（0，1】上的取值范围为（-∞，0】
即M=（0，1】，N=（-∞，0】
∴M∪N=（-∞，1】．
点评：本题考查了集合的知识，但更重要的还是对数函数和指数函数性质和图象的应用．