题目内容
以平面直角坐标系的原点为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位.已知直线l的参数方程是
(t为参数),圆C的极坐标方程是ρ=4cosθ,则直线l被圆C截得的弦长为( )
|
A、
| ||
B、2
| ||
C、
| ||
D、2
|
考点:点的极坐标和直角坐标的互化,直线与圆的位置关系,参数方程化成普通方程
专题:坐标系和参数方程
分析:先求出直线和圆的直角坐标方程,求出半径和弦心距,再利用弦长公式求得弦长.
解答:解:直线l的参数方程是
(t为参数),化为普通方程为 x-y-4=0;
圆C的极坐标方程是ρ=4cosθ,即ρ2=4ρcosθ,化为直角坐标方程为x2+y2=4x,
即 (x-2)2+y2=4,表示以(2,0)为圆心、半径r等于2的圆.
弦心距d=
=
<r,∴弦长为2
=2
=2
,
故选:D.
|
圆C的极坐标方程是ρ=4cosθ,即ρ2=4ρcosθ,化为直角坐标方程为x2+y2=4x,
即 (x-2)2+y2=4,表示以(2,0)为圆心、半径r等于2的圆.
弦心距d=
| |2-0-4| | ||
|
| 2 |
| r2-d2 |
| 4-2 |
| 2 |
故选:D.
点评:本题主要考查把参数方程化为普通方程的方法,把极坐标方程化为直角坐标方程的方法,点到直线的距离公式、弦长公式的应用,属于中档题.

练习册系列答案
相关题目
复数
(i为虚数单位)在复平面上对应的点在( )
| 2+i |
| i3 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知数列{an},若点{n,an}(n∈N*)在直线y+2=k(x-5)上,则数列{an}的前9项和S9=( )
| A、18 | B、-45 | C、22 | D、-18 |
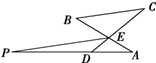 如图,AB与CD相交于点E,过E作BC的平行线与AD的延长线交于点P,已知∠A=∠C,PD=2DA=2,求PE的长.
如图,AB与CD相交于点E,过E作BC的平行线与AD的延长线交于点P,已知∠A=∠C,PD=2DA=2,求PE的长.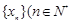 ,数列
,数列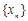 至少有两项)且
至少有两项)且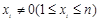 ,定义集合
,定义集合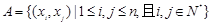 .若对任意点
.若对任意点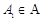 ,
,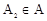 使得
使得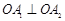
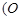 为坐标原点),则称数列
为坐标原点),则称数列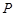 .
.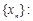 -2,2具有性质
-2,2具有性质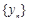 :-2,-1,1,3具有性质
:-2,-1,1,3具有性质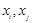 ,使得
,使得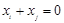 ;
;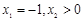 且
且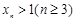 ,则
,则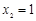 .
.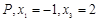 ,则
,则 .
.