��Ŀ����
��2006•��������ģ����ƽ��ֱ������ϵ�У���֪����
=��c��0����c��������c��0����
=��x��x����x��R����
|
|����СֵΪ 1 ��
=(
�� t)��aΪ��������a��c��t��R��������Pͬʱ��������������������1��|
|=
|
|����2��
=��
���ˡ�R���Ҧˡ�0������3������P�Ĺ켣C������B��0��-1����
����������C�ķ��̣�
�����Ƿ���ڷ�������Ϊ
=��1��k����k��0����ֱ��l��l������C�ཻ��M��N���㣬ʹ|
|=|
|����
��
�ļн�Ϊ60�㣿�����ڣ����kֵ����д��ֱ��l�ķ��̣��������ڣ���˵�����ɣ�
| OF |
| OG |
|
| FG |
| OE |
| a2 |
| c |
| PF |
| c |
| a |
| PE |
| PE |
| OF |
����������C�ķ��̣�
�����Ƿ���ڷ�������Ϊ
| m |
| BM |
| BN |
| BM |
| BN |
��������I������������ģ�ļ��㹫ʽ�Ͷ��κ����ĵ����Լ��ɵó�c����
=(
�� t) (t��R)����֪��E��ֱ�� x=
����
�ɣ�1������2������Բ�ĵڶ������֪����P�Ĺ켣C����Բ���ó����ɣ�
��II��������ڷ���������ֱ��l������l�ķ���Ϊ��y=kx+m��M��x1��y1����N��x2��y2������ֱ��l�ķ�������Բ���������ɵá���0������ϵ���Ĺ�ϵ�������ô�ֱƽ���ߵ����ʿɵ��߶�MN�Ĵ�ֱƽ���ߵķ��̣����ݡ�BMNΪ�ȱ������Σ��ɵõ�B��ֱ��MN�ľ���d=
|MN|�������õ㵽ֱ�ߵľ��빫ʽ���ҳ���ʽ���ɵó���
| OE |
| a2 |
| c |
| a2 |
| c |
�ɣ�1������2������Բ�ĵڶ������֪����P�Ĺ켣C����Բ���ó����ɣ�
��II��������ڷ���������ֱ��l������l�ķ���Ϊ��y=kx+m��M��x1��y1����N��x2��y2������ֱ��l�ķ�������Բ���������ɵá���0������ϵ���Ĺ�ϵ�������ô�ֱƽ���ߵ����ʿɵ��߶�MN�Ĵ�ֱƽ���ߵķ��̣����ݡ�BMNΪ�ȱ������Σ��ɵõ�B��ֱ��MN�ľ���d=
| ||
| 2 |
����⣺����|
|=
=
��
c��
��
c=1 �� ��c=
��
��
=(
�� t) (t��R)����֪��E��ֱ�� x=
����
�ɣ�1������2����֪��P��ֱ��x=
�����뵽��F�ľ���֮��Ϊ
(a��c��0)��
������Բ�ĵڶ������֪����P�Ĺ켣C����Բ��
����ԲC�ķ���Ϊ��
+
=1������b2=a2-c2��
�ɣ�3����֪b=1����a2=b2+c2=1+2=3������ԲC�ķ���Ϊ��
+y2=1��
��������ڷ���������ֱ��l������l�ķ���Ϊ��y=kx+m��M��x1��y1����N��x2��y2����
�� ��ȥy�� ��(1+3k2)x2+6kmx+3m2-3=0��
��x1+x2=-
�� x1x2=
��
��=36k2m2-12��m2-1����1+3k2��=12[3k2-m2+1]��0 ��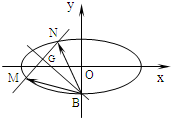
���߶�MN���е�G��x0��y0����x0=
=-
�� y0=kx0+m=-
+m=
��
�߶�MN�Ĵ�ֱƽ���ߵķ���Ϊ��y-
=-
(x+
)��
��|
|=|
|�����߶�MN�Ĵ�ֱƽ���߹�B��0��-1���㣮
��-1-
=-
•
=-
��
��m=
����
�ڴ���٣���3k2-��
)2+1��0 �� ���-1��k��1 �� ��k��0����
��|
|=|
|�� ��
��
�ļн�Ϊ60�㣬���BMNΪ�ȱ������Σ�
���B��ֱ��MN�ľ���d=
|MN|��
��d=
=
=
��
�֡�|MN|=
|x1-x2|=
•
=
•
=
�T
=3
��
��
=
��
���k2=
����k=��
�������ʽ������ڣ���m=
=
=1��
ֱ��l�ķ���Ϊ��y=��
x+1��
| FG |
| (x-c)2+x2 |
2(x-
|
| ||
| 2 |
��
| ||
| 2 |
| 2 |
��
| OE |
| a2 |
| c |
| a2 |
| c |
�ɣ�1������2����֪��P��ֱ��x=
| a2 |
| c |
| a |
| c |
������Բ�ĵڶ������֪����P�Ĺ켣C����Բ��
����ԲC�ķ���Ϊ��
| x2 |
| a2 |
| y2 |
| b2 |
�ɣ�3����֪b=1����a2=b2+c2=1+2=3������ԲC�ķ���Ϊ��
| x2 |
| 3 |
��������ڷ���������ֱ��l������l�ķ���Ϊ��y=kx+m��M��x1��y1����N��x2��y2����
|
��x1+x2=-
| 6km |
| 1+3k2 |
| 3m2-3 |
| 1+3k2 |
��=36k2m2-12��m2-1����1+3k2��=12[3k2-m2+1]��0 ��

���߶�MN���е�G��x0��y0����x0=
| x1+x2 |
| 2 |
| 3km |
| 1+3k2 |
| 3k2m |
| 1+3k2 |
| m |
| 1+3k2 |
�߶�MN�Ĵ�ֱƽ���ߵķ���Ϊ��y-
| m |
| 1+3k2 |
| 1 |
| k |
| 3km |
| 1+3k2 |
��|
| BM |
| BN |
��-1-
| m |
| 1+3k2 |
| 1 |
| k |
| 3km |
| 1+3k2 |
| 3m |
| 1+3k2 |
��m=
| 1+3k2 |
| 2 |
�ڴ���٣���3k2-��
| 1+3k2 |
| 2 |
��|
| BM |
| BN |
| BM |
| BN |
���B��ֱ��MN�ľ���d=
| ||
| 2 |
��d=
| |1+m| | ||
|
|1+
| ||
|
| 3 |
| 2 |
| 1+k2 |
�֡�|MN|=
| 1+k2 |
| 1+k2 |
| (x1+x2)2-4x1x2 |
=
| 1+k2 |
(-
|
|
| 12(3k2-m2+1) |
�T
| ||
| 1+3k2 |
12[3k2-(
|
| ||
|
| 1-k2 |
��
| 3 |
| 2 |
| 1+k2 |
3
| ||
| 2 |
| ||
|
| 1-k2 |
���k2=
| 1 |
| 3 |
| ||
| 3 |
| 1+3k2 |
| 2 |
| 1+1 |
| 2 |
ֱ��l�ķ���Ϊ��y=��
| ||
| 3 |
����������������Բ�ı����̼������ʡ�ֱ������Բ���ཻ����ת��Ϊ��ֱ�ߵķ�����˫���ߵķ��������ɵø���ϵ���Ĺ�ϵ������0���е����깫ʽ����������˼�뷽�����ǽ���Ĺؼ���

��ϰ��ϵ�д�
 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д� �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�
�����Ŀ
 ��2006•��������ģ������y=f��x����ͼ����ͼ��ʾ����y=f��x���ĵ�����y=f�䣨x����ͼ������ǣ�������
��2006•��������ģ������y=f��x����ͼ����ͼ��ʾ����y=f��x���ĵ�����y=f�䣨x����ͼ������ǣ������� ��2006•��������ģ����֪������������ABC-A1B1C1�У�AB=a��AA1=2a��D��E�ֱ��Dz���BB1��AC1���е㣮
��2006•��������ģ����֪������������ABC-A1B1C1�У�AB=a��AA1=2a��D��E�ֱ��Dz���BB1��AC1���е㣮