题目内容
15.函数f(x)=$\left\{\begin{array}{l}{lnx,(0<x≤1)}\\{2x+\frac{3}{x},(x>1)}\end{array}\right.$,若函数g(x)=f(x)-kx+k的零点有2个,则k的取值范围1<k≤2.分析 函数g(x)=f(x)-kx+k的零点个数,即函数f(x)与h(x)=k(x-1)图象交点的个数,画出函数的图象,数形结合可得答案.
解答 解:令g(x)=f(x)-kx+k=0,
∴f(x)=k(x-1),令h(x)=k(x-1),
画出函数f(x),h(x)的图象,
如图示:直线y=k(x-1)经过定点(1,0),斜率为k.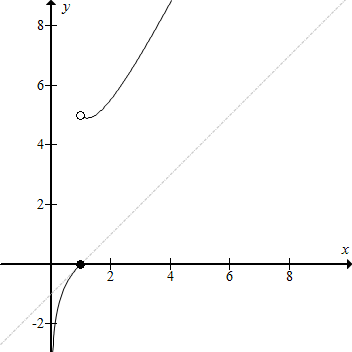
当 0<x<1时,
∴$f'(x)=\frac{1}{x}>1$,
当x≥1时,
∴$f'(x)=2-\frac{3}{x^2}∈({-\frac{3}{2},2})$,
若函数g(x)=f(x)-kx+k的零点有2个,
则函数f(x)与h(x)=k(x-1)图象交点有两个,
∴1<k≤2,
故答案为:1<k≤2
点评 本题考查的知识点是函数的零点,导函数的几何意义,根的存在性及个数的判断,转化比较困难,属于中档题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
5.已知f(x2)=log2x(x>0),那么f(16)等于( )
| A. | $\frac{1}{4}$ | B. | 4 | C. | 2 | D. | $\frac{1}{2}$ |
6.设a=2-1,b=log3$\frac{7}{81}$,c=($\frac{2}{3}$)-1,则( )
| A. | a>b>c | B. | b<a<c | C. | a<b<c | D. | b<c<a |
10.点A(1,2,3)关于xOy平面对称的点B坐标是( )
| A. | (-1,2,3) | B. | (1,-2,3) | C. | (1,2,-3) | D. | (-1,-2,3) |
4.若α≠$\frac{kπ}{2}$(k∈Z),则f(α)=$\frac{sinα+tanα}{cosα+cotα}$的取值情况是( )
| A. | 必取正值 | B. | 必取负值 | C. | 可取零值 | D. | 可正可负 |
