题目内容
若函数f(x)=a|2x-4|(a>0,a≠1)满足f(1)= ,则f(x)的单调递减区间是( )
,则f(x)的单调递减区间是( )
(A)(-∞,2] (B)[2,+∞)
(C)[-2,+∞) (D)(-∞,-2]
B
【解析】由f(1)=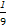 得a2=
得a2=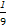 ,
,
∴a=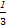 或a=-
或a=-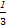 (舍),
(舍),
即f(x)=(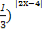 .由于y=|2x-4|在(-∞,2]上单调递减,在[2,+∞)上单调递增,所以f(x)在(-∞,2]上单调递增,在[2,+∞)上单调递减,故选B.
.由于y=|2x-4|在(-∞,2]上单调递减,在[2,+∞)上单调递增,所以f(x)在(-∞,2]上单调递增,在[2,+∞)上单调递减,故选B.

练习册系列答案
相关题目
题目内容
若函数f(x)=a|2x-4|(a>0,a≠1)满足f(1)= ,则f(x)的单调递减区间是( )
,则f(x)的单调递减区间是( )
(A)(-∞,2] (B)[2,+∞)
(C)[-2,+∞) (D)(-∞,-2]
B
【解析】由f(1)=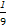 得a2=
得a2=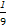 ,
,
∴a=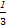 或a=-
或a=-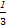 (舍),
(舍),
即f(x)=(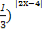 .由于y=|2x-4|在(-∞,2]上单调递减,在[2,+∞)上单调递增,所以f(x)在(-∞,2]上单调递增,在[2,+∞)上单调递减,故选B.
.由于y=|2x-4|在(-∞,2]上单调递减,在[2,+∞)上单调递增,所以f(x)在(-∞,2]上单调递增,在[2,+∞)上单调递减,故选B.
