Question

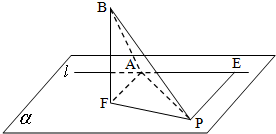如图，平面α上定点F到定直线l的距离FA=2，曲线C是平面α上到定点F和到定直线l的距离相等的动点P的轨迹． 设FB⊥α，且FB=2．
（1）若曲线C上存在点P₀，使得P₀B⊥AB，试求直线P₀B与平面α所成角θ的大小；
（2）对（1）中P₀，求点F到平面ABP₀的距离h．

Answer 1

分析：（1）解法一：以线段FA的中点为原点O，以线段FA所在的直线为x轴，建立空间直角坐标系O-xyz，由此易求出曲线C的方程，设出P点坐标后，根据P₀B⊥AB，构造方程，解方程求出P点坐标，即可得到答案．
解法二：以点A为原点O，以线段FA所在的直线为x轴，建立空间直角坐标系O-xyz．设出P点的坐标，根据曲线C是平面α上到定点F和到定直线l的距离相等的动点P的轨迹，构造方程，解方程求出P点坐标，即可得到答案．
（2）解法一：由（1）可得，△ABP的面积及△AFP的面积，然后使用等体积法，即可求出点F到平面ABP₀的距离h．
解法二：计算出平面ABP₀的一个法向量的坐标，代入点到平面距离公式，h=

| AF • n0 |

| n0 |

，即可求出点F到平面ABP₀的距离h．

解答：解：（1）（解法一）如图，以线段FA的中点为原点O，以线段FA所在的直线为x轴，建立空间直角坐标系O-xyz．
由题意，曲线C是平面α上以原点O为顶点，由于在xOy平面内，CF（2，0，0）
是以O为顶点，以x轴为对称轴的抛物线，其方程为y²=4x，
因此，可设P(

y2

4

，y，0)A（-1，0，0），B（1，0，2），所以，

AB

=(2，0，2)，

PB

=(1-

y2

4

，-y，2)．
由P₀B⊥AB，得2(1-

y2

4

)+4=0?y=2

3

，?P(3，2

3

，0)
所以，直线P₀B与平面α所成角的大小为arctan

1

2

（或arcsin

3

3

）．
（解法二）如图，以点A为原点O，以线段FA所在的直线为x轴，建立空间直角坐标系O-xyz．
所以，A（0，0，0），B（2，0，2），F（2，0，0），并设P（x，y，0），
由题意，

PB2+AB2=AP2 PF=PE.

(x-2)2+y2+4+8=x2+y2 (x-2)2+y2=x2.

?P(3，2

3

，0)
所以，直线P₀B与平面α所成角的大小为arctan

1

2

（或arcsin

5

5

）．
（2）（解法一）由（1），得△ABP的面积为S△ABP=2

10

，△AFP的面积为S△AFP=2

3

，
所以，

1

3

×2

10

h=

1

3

×2

3

×2，
解得，h=

30

5

．
（解法二）

AB

=(2，0，2)，

AP

=(4，2

3

，0)，设向量

n

=(x，y，z)
则

2x+2z=0 4x+2 3 y=0

所以，平面ABP₀的一个法向量

n0

=(3，-2

3

，-3)，∴h=

| AF • n0 |

| n0 |

=

30

5

．

点评：本题考查的知识点是直线与平面所成的角，点到平面的距离计算，其中（1）的关键是求出满足条件的P点坐标，（2）的中解法一关键是利用转化思想，根据棱锥翻转过程中体积不变进行求解，解法二的关键是点到平面距离公式，h=

| AF • n0 |

| n0 |

．