题目内容
如图,过S引三条长度相等但不共面的线段SA、SB、SC,且∠ASB=∠ASC=60°,∠BSC=90°.求证:平面ABC⊥平面BSC.
【探究】 本题可以用两种方法来证明,一是作平面的垂线而后证明它在另一个平面内(证法一);二是在一个平面内找一条线段,证明它与另一个平面垂直(证法二).
证法一:作AD⊥平面BSC,D为垂足.
∵∠ASB=∠ASC=60°,SA=SB=SC,则AS=AB=AC,
∴D为△BSC的外心.又∠BSC=90°,
∴D为BC的中点,即AD在平面ABC内.
∴平面ABC⊥平面BSC.
证法二:取BC的中点D,连结AD、SD,易证AD⊥BC.又△ABS是正三角形,△BSC为等腰直角三角形,∴BD=SD.∴AD2+SD2=AD2+BD2=AB2=AS2.
由勾股定理的逆定理,知AD⊥SD,∴AD⊥平面BSC.
又AD![]() 平面ABC,∴平面ABC⊥平面BSC.
平面ABC,∴平面ABC⊥平面BSC.
【规律总结】 本题是证明面面垂直的典型例题,关键是将证明“面面垂直”的问题转化为证明“线面垂直”的问题.

练习册系列答案
相关题目
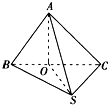 如图,过S引三条长度相等但不共面的线段SA、SB、SC,且∠ASB=∠ASC=60°,∠BSC=90°,求证:平面ABC⊥平面BSC.
如图,过S引三条长度相等但不共面的线段SA、SB、SC,且∠ASB=∠ASC=60°,∠BSC=90°,求证:平面ABC⊥平面BSC. 如图,过S引三条长度相等但不共面的线段SA、SB、SC,且∠ASB=∠ASC=60°,∠BSC=90°,求证:平面ABC⊥平面BSC.
如图,过S引三条长度相等但不共面的线段SA、SB、SC,且∠ASB=∠ASC=60°,∠BSC=90°,求证:平面ABC⊥平面BSC.
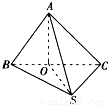 如图,过S引三条长度相等但不共面的线段SA、SB、SC,且∠ASB=∠ASC=60°,∠BSC=90°,求证:平面ABC⊥平面BSC.
如图,过S引三条长度相等但不共面的线段SA、SB、SC,且∠ASB=∠ASC=60°,∠BSC=90°,求证:平面ABC⊥平面BSC.