题目内容
设函数 ,若
,若 是从-1,0,1,2四数中任取一个,
是从-1,0,1,2四数中任取一个,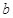 是从1,2,3,4,5五数中任取一个,那么
是从1,2,3,4,5五数中任取一个,那么 恒成立的概率为 ( ▲ )
恒成立的概率为 ( ▲ )
 ,若
,若 是从-1,0,1,2四数中任取一个,
是从-1,0,1,2四数中任取一个,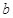 是从1,2,3,4,5五数中任取一个,那么
是从1,2,3,4,5五数中任取一个,那么 恒成立的概率为 ( ▲ )
恒成立的概率为 ( ▲ )A. | B. | C.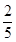 | D.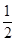 |
A
若 ,则
,则 ,则
,则 ,所以
,所以 单调递减,则当
单调递减,则当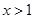 时
时 ,此时不存在符合条件的
,此时不存在符合条件的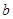 值;
值;
若 ,则
,则 ,当
,当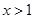 时
时 单调递减且
单调递减且 恒成立,此时
恒成立,此时 ;
;
若 ,则
,则 当且仅当
当且仅当 时取等号,所以此时
时取等号,所以此时 ;
;
若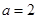 ,则
,则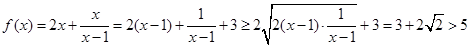 当且仅当
当且仅当 时取等号,所以此时
时取等号,所以此时 。
。
综上可得,使得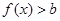 恒成立的
恒成立的 取值为
取值为 ,
, 和
和 共9组,所以概率为
共9组,所以概率为 ,故选A
,故选A
 ,则
,则 ,则
,则 ,所以
,所以 单调递减,则当
单调递减,则当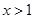 时
时 ,此时不存在符合条件的
,此时不存在符合条件的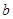 值;
值;若
 ,则
,则 ,当
,当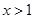 时
时 单调递减且
单调递减且 恒成立,此时
恒成立,此时 ;
;若
 ,则
,则 当且仅当
当且仅当 时取等号,所以此时
时取等号,所以此时 ;
;若
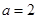 ,则
,则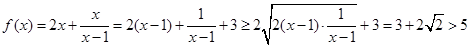 当且仅当
当且仅当 时取等号,所以此时
时取等号,所以此时 。
。综上可得,使得
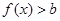 恒成立的
恒成立的 取值为
取值为 ,
, 和
和 共9组,所以概率为
共9组,所以概率为 ,故选A
,故选A
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 , x
, x ,x
,x
 R,且x
R,且x 的图象必过定点( )
的图象必过定点( )



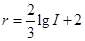 。1976年7月28日,我国唐山发生了里氏震级为7.8级的地震,它所释放的相对能量是2010年2月27日智利地震所散发的相对能量的
。1976年7月28日,我国唐山发生了里氏震级为7.8级的地震,它所释放的相对能量是2010年2月27日智利地震所散发的相对能量的 倍,那么智利地震的里氏震级是 级。(取lg2=0.3)
倍,那么智利地震的里氏震级是 级。(取lg2=0.3) 、
、 两点满足条件:①点
两点满足条件:①点 图像上;②点
图像上;②点
 ,则
,则 在区间
在区间
 为整数)上的值域是
为整数)上的值域是 ,则满足条件的数对
,则满足条件的数对 共有 ▲ 对;
共有 ▲ 对; 的方程组
的方程组 有两组不同的解,则实数
有两组不同的解,则实数 的取值范围是____________.
的取值范围是____________.