题目内容
已知函数f（x）=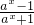
（a＞0且a≠1）．
（1）求f（x）的定义域和值域；
（2）讨论f（x）的单调性．
解：（1）易得f（x）的定义域为{x|x∈R}．设y=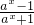，解得ax=-
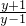①
∵ax＞0当且仅当-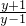＞0时，方程①有解．解-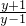＞0得-1＜y＜1．
∴f（x）的值域为{y|-1＜y＜1}．
（2）f（x）=
=1-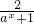
．
1°当a＞1时，∵ax+1为增函数，且ax+1＞0．
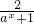∴为减函数，从而f（x）=1-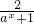=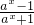为增函数．
2°当0＜a＜1时，类似地可得f（x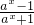）=为减函数．
分析：（1）定义域易得，利用反解自变量的方法求值域即可．
（2）先把函数分离常数，在分底数和1的大小两种情况再结合复合函数的单调性来判断即可．
点评：本题是对函数定义域和值域以及单调性的综合考查．在利用复合函数的单调性时，其原则是；单调性相同为增，单调性相反为减，且乘正数单调性不变，乘负数单调性相反．
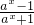，解得ax=-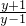①∵ax＞0当且仅当-
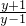＞0时，方程①有解．解-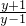＞0得-1＜y＜1．∴f（x）的值域为{y|-1＜y＜1}．
（2）f（x）=
=1-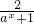．1°当a＞1时，∵ax+1为增函数，且ax+1＞0．
∴
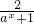为减函数，从而f（x）=1-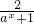=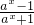为增函数．2°当0＜a＜1时，类似地可得f（x）=
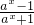为减函数．分析：（1）定义域易得，利用反解自变量的方法求值域即可．
（2）先把函数分离常数，在分底数和1的大小两种情况再结合复合函数的单调性来判断即可．
点评：本题是对函数定义域和值域以及单调性的综合考查．在利用复合函数的单调性时，其原则是；单调性相同为增，单调性相反为减，且乘正数单调性不变，乘负数单调性相反．
练习册系列答案
冲刺100分单元优化练考卷系列答案
相关题目
已知函数f（x）=x2-bx的图象在点A（1，f（1））处的切线l与直线3x-y+2=0平行，若数列{
}的前n项和为Sn，则S2010的值为（ ）
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|