题目内容
已知某几何体的直观图和三视图如下图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,
(1)求证:BC∥平面C1B1N;
(2)求证:BN⊥平面C1B1N;
(3)求此几何体的体积.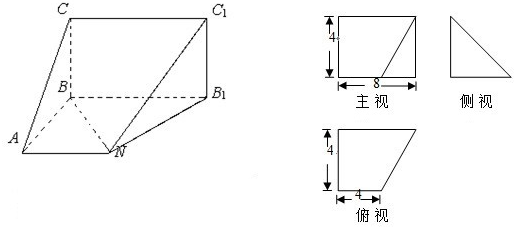
(1)求证:BC∥平面C1B1N;
(2)求证:BN⊥平面C1B1N;
(3)求此几何体的体积.

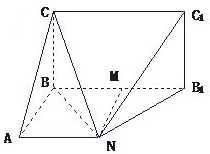
(1)证明:∵该几何体的正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,∴BA,BC,BB1两两互相垂直.
∵BC∥B1C1,B1C1?平面C1B1N,BC?平面C1B1N,
∴BC∥平面C1B1N…(4分)
(2)连BN,过N作NM⊥BB1,垂足为M,
∵B1C1⊥平面ABB1N,BN?平面ABB1N,
∴B1C1⊥BN,…(5分)
由三视图知,BC=4,AB=4,BM=AN=4,BA⊥AN,
∴BN=
| 42+42 |
| 2 |
| NM2+B1M2 |
| 42+42 |
| 2 |
∵BB1=82=64,B1N2+BN2=32+32=64,
∴BN⊥B1N,…(7分)
∵B1C1?平面B1C1N,B1N?平面B1C1N,B1N∩B1C1=B1
∴BN⊥平面C1B1N …(9分)
(3)连接CN,
VC-BCN=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 32 |
| 3 |
∴平面B1C1CB⊥ANB1B=BB1,NM⊥BB1,NM?平面B1C1CB,
∴NM⊥平面B1C1CB,
V N-B1C1CB=
| 1 |
| 3 |
| 1 |
| 3 |
| 128 |
| 3 |
此几何体的体积V=VC-BCN+V N-B1C1CB=
| 32 |
| 3 |
| 64 |
| 3 |
V=VC-BCN+V N-B1C1CB=
| 32 |
| 3 |
| 128 |
| 3 |
| 160 |
| 3 |

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目





