Question

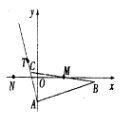
【题目】如图，已知的边所在直线的方程为，满足，点在边所在直线上且满足.

（1）求边所在直线的方程；

（2）求外接圆的方程；

（3）若动圆过点，且与的外接圆外切，求动圆的圆心的轨迹方程.

Answer 1

【答案】（1）；（2）；（3）.

【解析】

试题分析：（1）由已知可得为，由边所在直线的方程为，可求直线的斜率，点在直线上，利用直线的点斜式可求；（2）与的交点，联立方程可求的坐标，由结合直角三角形的性质可得的外接圆的圆心，进而可求，外接圆的方程可求；（3）由题意可得，即，结合圆锥曲线的定义可求轨迹方程.

试题解析：（1），又在上，

，为，

又边所在直线的方程为，所以直线的斜率为，又因为点

在直线上，所以边所在直线的方程为：，即.

（2）与的交点为，所以由

解得点的坐标为，，为斜边上的中点，即为外接圆的圆心，又，

从而外接圆的方程为:.

（3）因为动圆过点，所以是该圆的半径，又因为动圆与圆外切，

所以，即.

故点的轨迹是以，为焦点，实轴长为的双曲线的左支.

因为实半轴长，半焦距.

所以虚半轴长.

从而动圆的圆心的轨迹方程为.