题目内容
在Rt△ABC中，CD是斜边上的高线，AC：BC=3：1则S△ABC：S△ACD为（ ）
| A、4：3 | B、9：1 | C、10：1 | D、10：9 |
分析：先设BC=a，则AC=3a，AB=
=
a，求出BD，CD的长，即可求出
，进而求出结论．（当然也可以直接求CD，AD）．（也可以先证其相似，再用相似比来解决）．
| a2+(3a)2 |
| 10 |
| S△ABC |
| S△BCD |
解答：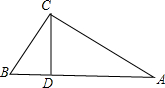
解：设BC=a，则AC=3a，AB=
=
a，
因为：BC2=BD•BA⇒BD=
=
a．
所以：CD=
=
=
a．
∴
=
=
=
．
∴
=
故选：D．
解：设BC=a，则AC=3a，AB=| a2+(3a)2 |
| 10 |
因为：BC2=BD•BA⇒BD=
| BC2 |
| AB |
| ||
| 10 |
所以：CD=
| CB2-BD2 |
a2-(
|
3
| ||
| 10 |
∴
| S△ABC |
| S△BCD |
| ||
|
| a•3a | ||||||||
|
| 10 |
| 1 |
∴
| S△ABC |
| S△ACD |
| 10 |
| 9 |
故选：D．
点评：本题主要考查直角三角形的射影定理的应用．考查计算能力，属于基础题目．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
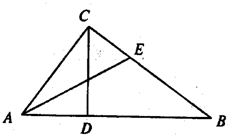如图，在Rt△ABC中，∠C是直角，AC=3，BC=4，CD⊥AB于点D，∠A的平分线交CD于点M，交BC于点E，求：
如图1，在Rt△ABC中，∠C=90°，BC=3，AC=6．D、E分别是AC、AB上的点，且DE∥BC，将△ADE沿DE折起到△A1DE的位置，使A1D⊥CD，如图2．
选修4-1：几何证明选讲