题目内容
四面体ABCD中,AD与BC互相垂直,AD=2BC=4,且AB+BD=AC+CD=2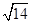 ,则四面体ABCD的体积的最大值是( )
,则四面体ABCD的体积的最大值是( )
| A.4 | B.2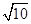 | C.5 | D.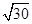 |
A
解析试题分析:
作 于
于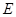 ,连接
,连接 ,则
,则 ,所以
,所以 ,由题设,
,由题设, 都是以
都是以 为焦点的椭圆上,且
为焦点的椭圆上,且 、
、 都垂直于焦距
都垂直于焦距 , AB+BD=AC+CD=2
, AB+BD=AC+CD=2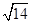 ,显然
,显然 ≌
≌ ,所以
,所以 ,取
,取 中点
中点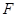 ,所以
,所以 ,
, ,四面体
,四面体 的体积取最大值,只需
的体积取最大值,只需 最大即可,当
最大即可,当 是等腰直角三角形时几何体的体积最大,因为 AB+BD=AC+CD=2
是等腰直角三角形时几何体的体积最大,因为 AB+BD=AC+CD=2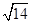 ,所以
,所以 ,所以
,所以 ,
, ,所以该几何体的体积为:
,所以该几何体的体积为: ,选A.
,选A.
考点:棱锥的体积.

练习册系列答案
相关题目
一个几何体的三视图如图所示,则该几何体的表面积是 ( )
A.4+2 | B.4+ | C.4+2 | D.4+ |













 ,得到三棱锥C-ABD,其正视图与俯视图为全等的等腰直角三角形,如图所示,则侧视图的面积为( )
,得到三棱锥C-ABD,其正视图与俯视图为全等的等腰直角三角形,如图所示,则侧视图的面积为( )



 的半圆,俯视图是半径为
的半圆,俯视图是半径为