题目内容
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，0＜φ＜π）的图象在y轴右侧的第一个最高点是(
，2)，且其与x轴正半轴的第一个交点是(
，0)．
（1）求f（x）的解析式；
（2）画出函数f（x）在一个周期上的简图．
| π |
| 12 |
| π |
| 4 |
（1）求f（x）的解析式；
（2）画出函数f（x）在一个周期上的简图．
分析：（1）根据题意可得振幅A=2，由T=4(
-
)=
，可知ω=3，由3×
+φ=
+2kπ，k∈Z，0＜φ＜π可求得f（x）的解析式；
（2）得到f（x）=2sin（3x+
）（x∈R）后，可列表，令3x+
=0，
，π，
，2π得到相应的x的值与y的值，用描点法作图即可．
| π |
| 4 |
| π |
| 12 |
| 2π |
| 3 |
| π |
| 12 |
| π |
| 2 |
（2）得到f（x）=2sin（3x+
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| 3π |
| 2 |
解答：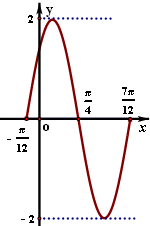
解：（1）由题知，振幅A=2，周期T=4(
-
)=
，即知ω=3．…（3分）
由最高点得3×
+φ=
+2kπ，k∈Z，即φ=
+2kπ，k∈Z…（6分）
由知0＜φ＜π，所以φ=
得f(x)=2sin(3x+
)，(x∈R)…（9分）
（2）列表
描点、连线得函数f（x）的图象如图．
【评分细则】坐标系完整即x、o、y及箭头齐全 （11分）
五点列表正确 （13分）
描点正确图象美观 （15分）
解：（1）由题知，振幅A=2，周期T=4(| π |
| 4 |
| π |
| 12 |
| 2π |
| 3 |
由最高点得3×
| π |
| 12 |
| π |
| 2 |
| π |
| 4 |
由知0＜φ＜π，所以φ=
| π |
| 4 |
得f(x)=2sin(3x+
| π |
| 4 |
（2）列表
3x+
|
0 |
|
π |
|
2π | ||||||||||
| x | -
|
|
|
|
| ||||||||||
| f（x） | 0 | 2 | 0 | -2 | 0 |
【评分细则】坐标系完整即x、o、y及箭头齐全 （11分）
五点列表正确 （13分）
描点正确图象美观 （15分）
点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式与五点法作函数y=Asin（ωx+φ）的图象，着重考查y=Asin（ωx+φ）的振幅、周期与初相的确定及五点法作图，属于中档题．
练习册系列答案
相关题目