题目内容
下列四个命题:
①命题“若x2-3x+2=0,x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”;
②若命题p:“?x∈R,使得x2+x+1<0.”则¬P:“?x∈R,x2+x+1≥0”;
③对于平面向量 ,
, ,
, ,若
,若  ,则
,则 ;
;
④已知u,v为实数,向量 ,
, 不共线,则u
不共线,则u +v
+v =0的充要条件是u=v=0.
=0的充要条件是u=v=0.
其中真命题有________(填上所有真命题的序号).
①②④
分析:①根据命题“若p,则q”的逆否命题是“若¬q,则¬p”可判断出原命题的逆否命题的真假;
②根据命题“?x∈R,结论p成立”的非命题是“?x∈R,结论p的反面成立”可判断出其真假;
③若 不垂直,则
不垂直,则 ,可知③的真假;
,可知③的真假;
④我们知道:当u=v=0时, ;若向量
;若向量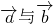 不共线,由
不共线,由 ,则u=v=0,由上可知④的真假.
,则u=v=0,由上可知④的真假.
解答:①根据命题“若p,则q”的逆否命题是“若¬q,则¬p”可知:命题“若x2-3x+2=0,x=1”的逆否命题
应为“若x≠1,则x2-3x+2≠0”,因此①是真命题;
②根据命题“?x∈R,结论q成立”的非命题是“?x∈R,结论q的反面成立”可知:若命题p:“?x∈R,使得x2+x+1<0.”则¬P是:“?x∈R,x2+x+1≥0”,故②是真命题;
③若 不垂直,则
不垂直,则 ,可知③是假命题;
,可知③是假命题;
④我们知道:当u=v=0时, ;若向量
;若向量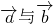 不共线,由
不共线,由 ,则u=v=0,由上可知:若u,v为实数,向量
,则u=v=0,由上可知:若u,v为实数,向量 ,
, 不共线,
不共线, 的充要条件是u=v=0.因此④是真命题.
的充要条件是u=v=0.因此④是真命题.
故真命题是①②④.
点评:本题以方程、不等式、向量为载体综合考查了四种命题、非命题及充要条件,准确掌握以上知识是解决问题的关键.
分析:①根据命题“若p,则q”的逆否命题是“若¬q,则¬p”可判断出原命题的逆否命题的真假;
②根据命题“?x∈R,结论p成立”的非命题是“?x∈R,结论p的反面成立”可判断出其真假;
③若
 不垂直,则
不垂直,则 ,可知③的真假;
,可知③的真假;④我们知道:当u=v=0时,
 ;若向量
;若向量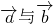 不共线,由
不共线,由 ,则u=v=0,由上可知④的真假.
,则u=v=0,由上可知④的真假.解答:①根据命题“若p,则q”的逆否命题是“若¬q,则¬p”可知:命题“若x2-3x+2=0,x=1”的逆否命题
应为“若x≠1,则x2-3x+2≠0”,因此①是真命题;
②根据命题“?x∈R,结论q成立”的非命题是“?x∈R,结论q的反面成立”可知:若命题p:“?x∈R,使得x2+x+1<0.”则¬P是:“?x∈R,x2+x+1≥0”,故②是真命题;
③若
 不垂直,则
不垂直,则 ,可知③是假命题;
,可知③是假命题;④我们知道:当u=v=0时,
 ;若向量
;若向量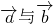 不共线,由
不共线,由 ,则u=v=0,由上可知:若u,v为实数,向量
,则u=v=0,由上可知:若u,v为实数,向量 ,
, 不共线,
不共线, 的充要条件是u=v=0.因此④是真命题.
的充要条件是u=v=0.因此④是真命题.故真命题是①②④.
点评:本题以方程、不等式、向量为载体综合考查了四种命题、非命题及充要条件,准确掌握以上知识是解决问题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目

 ,则
,则 ”的逆否命题为假命题;
”的逆否命题为假命题; :任意
:任意 ,都有
,都有 ,则“非
,则“非 ,使
,使 ;
; ”是“函数
”是“函数 为偶函数”的充要条件;
为偶函数”的充要条件; ;
; :△ABC中,
:△ABC中, ,那么命题“‘非
,那么命题“‘非 B.
B. C.
C. D.
D.
 是奇函数,则下列命题是真命题的是( )
是奇函数,则下列命题是真命题的是( )