题目内容
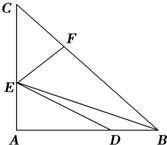 已知:如图,△ABC中,AB=AC,∠BAC=90°,AE=
已知:如图,△ABC中,AB=AC,∠BAC=90°,AE=| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
(1)EF⊥BC;
(2)∠ADE=∠EBC.
分析:(1)设AB=3,以点A为坐标原点,以AB所在的直线为x轴,以AC所在的直线为y轴,建立直角坐标系,从而可得到E,F,B,C的坐标,利用向量的数量积即可证得EF⊥BC;
(2)利用
•
与
•
数量积中的夹角的余弦即可证得∠ADE=∠EBC.
(2)利用
| DE |
| DA |
| BE |
| BC |
解答:解:(1)设AB=3,以点A为坐标原点,以AB所在的直线为x轴,以AC所在的直线为y轴,建立直角坐标系,
则E(0,1),F(1,2),B(3,0),C(0,3),
∴
=(1,1),
=(-3,3)
∵
•
=-3+3=0,
∴EF⊥BC;
(2)∵D(2,0),A(0,0),
∴
=(-2,1),
=(-2,0),
∴|
|=
,|
|=2,又
•
=4,
∴cos<
,
>=
=
=
,
同理可求cos<
,
>=
,
∴<
,
>=<
,
>,
∴∠ADE=∠EBC.
则E(0,1),F(1,2),B(3,0),C(0,3),
∴
| EF |
| BC |
∵
| EF |
| BC |
∴EF⊥BC;
(2)∵D(2,0),A(0,0),
∴
| DE |
| DA |
∴|
| DE |
| 5 |
| DA |
| DE |
| DA |
∴cos<
| DE |
| DA |
| ||||
|
|
| 4 | ||
2
|
2
| ||
| 5 |
同理可求cos<
| BE |
| BC |
2
| ||
| 5 |
∴<
| DE |
| DA |
| BE |
| BC |
∴∠ADE=∠EBC.
点评:本题考查数量积表示两个向量的夹角,考查建立坐标系利用数量积判断两个平面向量的垂直关系,属于中档题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
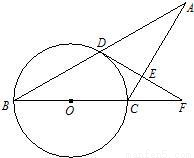
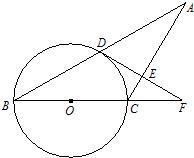 9、已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F.
9、已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F. 已知:如图,△ABC中,∠B=60°,AD,CE是角平分线.
已知:如图,△ABC中,∠B=60°,AD,CE是角平分线.