题目内容
设m>2,给定数列{x n },其中x 1=m,xn+1=
(n∈N+),求证:x n>2且
<1.
| xn2 |
| 2(xn-1) |
| xn+1 |
| xn |
分析:x n>2且
<1等价于证明2<xn+1<xn.结合题设条件x 1=m>2,xn+1=
(n∈N+),利用数学归纳法进行证明.
| xn+1 |
| xn |
| xn2 |
| 2(xn-1) |
解答:解:x n>2且
<1等价于证明2<xn+1<xn.
下面用数学归纳法进行证明:
①当n=1时,
∵x2=
=x1+
,
x2=
=
=2+
,x1=m>2,
∴2<x2<x1.
结论成立.
②假设n=k时,结论成立,即2<xk+1<xk(k∈N+),
则xk+2=
=xk+1+
>xk+1,
xk+2=
=2+
>2.
∴2<xk+2<xk+1,
综上所述,由①②知2<xn+1<xn.
∴x n>2且
<1.
| xn+1 |
| xn |
下面用数学归纳法进行证明:
①当n=1时,
∵x2=
| x12 |
| 2(x1-1) |
| (2-x1)x1 |
| 2(x1-1) |
x2=
| x12 |
| 2(x1-1) |
| 4(x1-1)+x12 -4x1+4 |
| 2(x1-1) |
| (x1-2)2 |
| 2(x1-1) |
∴2<x2<x1.
结论成立.
②假设n=k时,结论成立,即2<xk+1<xk(k∈N+),
则xk+2=
| xk+12 |
| 2(xk+1-1) |
| (2-xk+1)xk+1 |
| 2(xk+1-1) |
xk+2=
| xk+12 |
| 2(xk+1-1) |
| (xk+1-2)2 |
| 2(xk+1-1) |
∴2<xk+2<xk+1,
综上所述,由①②知2<xn+1<xn.
∴x n>2且
| xn+1 |
| xn |
点评:本题考查数列与不等式的综合应用,综合性强,难度大,容易出错.解题时要认真审题,注意数学归纳法的合理运用.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
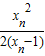 (n∈N+),求证:x n>2且
(n∈N+),求证:x n>2且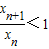 .
.