Question

数列{a_n}的首项为a₁=2，且，记S_n为数列{a_n}前n项和，则S_n=　　．

Answer 1

考点：

数列的求和．

专题：

计算题．

分析：

观察已知可得，两式相减可得{a_n}是从第二项开始的等比数列，代入等比数列的前n和公式求解

解答：

解：由题意可得

当n两式相减得，

从而有，

数列 a_n从第二项开始的等比数列，公比为

∴S_n=a₁+a₂+a₃+…+a_n=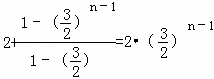

故答案为：

点评：

本题主要考查了由数列的递推公式求解数列的通项公式，等比数列的求和公式，运用递推公式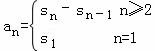时，要检验a₁的值是否适合a_n（n≥2），而本题中的a_n是从第二项开始的等比数列，在求和时，要分组进行求和．