题目内容
(2012•黄州区模拟)已知向量
=(cos
,-1),
=(
sin
,cos2
),设函数f(x)=
•
+
.
(1)若x∈[0,
],f(x)=
,求cosx的值;
(2)在△ABC中,角A,B,C的对边分别是a,b,c,且满足2bcosA≤2c-
a,求f(B)的取值范围.
| m |
| x |
| 2 |
| n |
| 3 |
| x |
| 2 |
| x |
| 2 |
| m |
| n |
| 1 |
| 2 |
(1)若x∈[0,
| π |
| 2 |
| ||
| 3 |
(2)在△ABC中,角A,B,C的对边分别是a,b,c,且满足2bcosA≤2c-
| 3 |
分析:(1)依题意得f(x)=
•
+
=sin(x-
)=
,由 x∈[0,
],sin(x-
)=
>0,cos(x-
)=
,由cosx=cos[(x-
)+
]利用两角和的余弦公式求得结果.
(2)由2bcosA≤2c-
a 得:cosB≥
,从而 0<B≤
,由此求得f(B)=sin(B-
)的取值范围.
| m |
| n |
| 1 |
| 2 |
| π |
| 6 |
| ||
| 3 |
| π |
| 2 |
| π |
| 6 |
| ||
| 3 |
| π |
| 6 |
| ||
| 3 |
| π |
| 6 |
| π |
| 6 |
(2)由2bcosA≤2c-
| 3 |
| ||
| 2 |
| π |
| 6 |
| π |
| 6 |
解答:解:(1)依题意得f(x)=
•
+
=
sin
cos
-cos2
+
=
sinx-
+
=sin(x-
),…(2分)
由 x∈[0,
],得:-
≤x-
≤
,sin(x-
)=
>0,
从而可得 cos(x-
)=
,…(4分)
则cosx=cos[(x-
)+
]=cos(x-
) sin
-sin(x-
) cos
=
-
. …(6分)
(2)在△ABC中,由2bcosA≤2c-
a 得 2sinBcosA≤2sin(A+B)-
sinA,即 2sinAcosB≥
sinA,
由于sinA>0,故有cosB≥
,从而 0<B≤
,…(10分)
故f(B)=sin(B-
),由于 0<B≤
,∴-
<B-
≤0,∴sin(B-
)∈(-
,0],即f(B)∈(-
,0]. …(12分)
| m |
| n |
| 1 |
| 2 |
| 3 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1+cosx |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
由 x∈[0,
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| ||
| 3 |
从而可得 cos(x-
| π |
| 6 |
| ||
| 3 |
则cosx=cos[(x-
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| ||
| 2 |
| ||
| 6 |
(2)在△ABC中,由2bcosA≤2c-
| 3 |
| 3 |
| 3 |
由于sinA>0,故有cosB≥
| ||
| 2 |
| π |
| 6 |
故f(B)=sin(B-
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查三角函数的恒等变换及化简求值,两角和的余弦公式,两个向量的数量积公式的应用,属于中档题.

练习册系列答案
相关题目
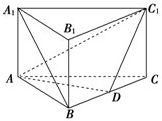 (2012•黄州区模拟)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1,∠ABC=90°,D是BC的中点.
(2012•黄州区模拟)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1,∠ABC=90°,D是BC的中点. (2012•黄州区模拟)已知某几何体的三视图如图,则该几何体的表面积为
(2012•黄州区模拟)已知某几何体的三视图如图,则该几何体的表面积为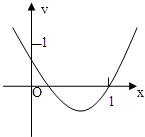 (2012•黄州区模拟)如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=2lnx+f(x)在点(b,g(b))处切线的斜率的最小值是( )
(2012•黄州区模拟)如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=2lnx+f(x)在点(b,g(b))处切线的斜率的最小值是( )