题目内容
设数列{an}的前n项和为Sn，令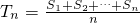
，称Tn为数列a1，a2，…，an的“理想数”，已知数列a1，a2，…，a500的“理想数”为2004，那么数列12，a1，a2，…，a500的“理想数”为
- A.2002
- B.2004
- C.2008
- D.2012
D
分析：由题意，数列a1，a2，…，a500的“理想数”为T500=
=2004，可得s1+s2+…+s500的值；
所以数列12，a1，a2，…，a500的“理想数”为T501=
，从而求出答案．
解答：根据题意，数列a1，a2，…，a500的“理想数”为：
T500==2004，∴s1+s2+…+s500=2004×500；
所以，数列12，a1，a2，…，a500的“理想数”为：
T501==
=2012．
故选：D．
点评：本题考查了数列新定义的求和问题的应用，解题时须认真分析，从题目中寻找解答问题的关键，从而得出答案．
分析：由题意，数列a1，a2，…，a500的“理想数”为T500=
=2004，可得s1+s2+…+s500的值；所以数列12，a1，a2，…，a500的“理想数”为T501=
，从而求出答案．解答：根据题意，数列a1，a2，…，a500的“理想数”为：
T500=
=2004，∴s1+s2+…+s500=2004×500；所以，数列12，a1，a2，…，a500的“理想数”为：
T501=
==2012．故选：D．
点评：本题考查了数列新定义的求和问题的应用，解题时须认真分析，从题目中寻找解答问题的关键，从而得出答案．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目