Question

如图，四棱锥P-ABCD中，侧面PDC是边长为2的正三角形，且与底面垂直，底面ABCD是∠ADC=60°的菱形，M为PB的中点.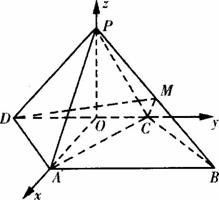

(Ⅰ)求PA与底面ABCD所成角的大小；

(Ⅱ)求证：PA⊥平面CDM；

(Ⅲ)求二面角D-MC-B的余弦值.

Answer 1

解：(1)取0C的中点O,由△PDC是正三角形,有PO⊥DC.又∵平面PDC⊥底面ABCD,∴PO⊥平面ABCD于O.连接OA,则OA是PA在底面上的射影.∴∠PAO就是PA与底面所成角.∵∠ADC=60°,由已知△PCD和△ACD是全等的正三角形,从而求得OA=OP=.  ∴∠PAO=45°.∴PA与底面ABCD可成角的大小为45°.

(Ⅱ)由底面ABCD为菱形且∠ADC=60°,DC=2,DO=1,

有OA⊥DC.建立空间直角坐标系如图,则

A(,0,0),P(0,0,),D(0,-1,0),B(,2,0),C(0,1,0).由M为PB中点,∴M(,1,).

∴=(,2,),=(,0,),=(0,2,0).

∴=×+2×0+()=0,=0×+2×0+0×()=0.

∴PA⊥DC,PA⊥DC.  ∴PA⊥平面DMC.

(Ⅲ)=(,0,),=(,1,0).令平面BMC的法向量n=(x,y,z),

则n·=0,从而x+z=0；    ①

n·=0,从而=0.    ②

由①②,取x=-1,则y=,z=1.  ∴可取n=(-1,,1).

由(Ⅱ)知平面CDM的法向量可取=(,0,),

∴cos=

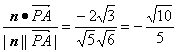
∴所求二面角的余弦值为.