题目内容
11.在△ABC中,已知A=45°,B=30°,c=10,求b.分析 利用三角形的内角和求出C,利用正弦定理和题设中一边和两个角的值求得a,通过正弦定理求出b即可.
解答 解:在△ABC中,∵A=45°,B=30°,c=10,
∴C=180°-A-B=105°,可得:sinC=sin(A+B)=sinAcosB+cosAsinB=$\frac{\sqrt{2}}{2}×\frac{\sqrt{3}}{2}+\frac{\sqrt{2}}{2}×\frac{1}{2}$=$\frac{\sqrt{6}+\sqrt{2}}{4}$,
∴由正弦定理可得:a=$\frac{csinA}{sinC}$=$\frac{10×\frac{\sqrt{2}}{2}}{\frac{\sqrt{6}+\sqrt{2}}{4}}$=10$\sqrt{3}$-10,
∴由正弦定理可得:b=$\frac{csinB}{sinC}$=$\frac{10×\frac{1}{2}}{\frac{\sqrt{6}+\sqrt{2}}{4}}$=5$\sqrt{6}$-5$\sqrt{2}$.
点评 本题给出三角形的两个角和一条边,解此三角形.着重考查了三角形内角和定理、特殊角的三角函数和正弦定理等知识,属于基础题.

练习册系列答案
相关题目
3.已知数列{an}的前n项和Sn满足:Sn+Sm=Sn+m,且a2=3,那么a12等于( )
| A. | 3 | B. | 6 | C. | 9 | D. | 12 |

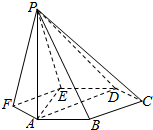 如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的是(4).
如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的是(4).