Question

直三棱柱ABC-A₁B₁C₁的六个顶点都在球O的球面上．若AB=BC=2，∠ABC=90°，AA₁=2

2

，则球O的表面积为

 

．

Answer 1

分析：根据直三棱柱的六个顶点都在球O的球面上，构造长方体，则长方体的体对角线即为球的直径，然后求出球的半径，即可求球的表面积．

解答：解：∵直三棱柱ABC-A₁B₁C₁的六个顶点都在球O的球面上，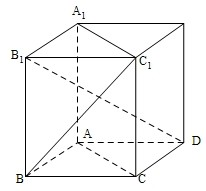
且AB=BC=2，∠ABC=90°，AA₁=2

2

，
∴构造长方体，则长方体的外接球和直三棱柱ABC-A₁B₁C₁的外接球是相同的，
则长方体的体对角线等于球的直径2R，
则2R=

22+22+(2 2 )2

=

16

=4，
∴R=2，
则球O的表面积为4πR²=4π×2²=16π，
故答案为：16π．

点评：本题主要考查空间几何体的位置关系，利用直三棱柱构造长方体是解决本题的关键，利用长方体的体对角线等于球的直径是本题的突破点．