题目内容
A、B是直线y=1与函数f(x)=2cos2
+cos(ωx+
)(ω>0)图象的两个相邻交点,且|AB|=
.
(1)求ω的值;
(2)在锐角△ABC中,a,b,c分别是角A,B,C的对边,若f(A)=-
,c=3,△ABC的面积为3
,求a的值.
| ωx |
| 2 |
| π |
| 3 |
| π |
| 2 |
(1)求ω的值;
(2)在锐角△ABC中,a,b,c分别是角A,B,C的对边,若f(A)=-
| 1 |
| 2 |
| 3 |
(1)f(x)=1+cosωx+
ωx-
sinωx=1-
sin(ωx-
).
由函数的图象及|AB|=
,得函数的周期T=
=2×
,解得ω=2;
(2)∵f(A)=1-
sin(2A-
)=-
.
∴sin(2A-
)=
.
又∵△ABC是锐角三角形,-
<2A-
<
,
∴2A-
=
,即A=
.
由S△ABC=
bcsinA=
×
=3
,得b=4由余弦定理,
得a2=b2+c2-2bccosA=42+32-2×4×3×
=13,即a=
.
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| π |
| 3 |
由函数的图象及|AB|=
| π |
| 2 |
| 2π |
| ω |
| π |
| 2 |
(2)∵f(A)=1-
| 3 |
| π |
| 3 |
| 1 |
| 2 |
∴sin(2A-
| π |
| 3 |
| ||
| 2 |
又∵△ABC是锐角三角形,-
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
∴2A-
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
由S△ABC=
| 1 |
| 2 |
| 3b |
| 2 |
| ||
| 2 |
| 3 |
得a2=b2+c2-2bccosA=42+32-2×4×3×
| 1 |
| 2 |
| 13 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (ω>0)图象的两个相邻交点,且
(ω>0)图象的两个相邻交点,且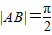 .
. 的面积为
的面积为 ,求a的值.
,求a的值. (ω>0)图象的两个相邻交点,且
(ω>0)图象的两个相邻交点,且 .
. 的面积为
的面积为 ,求a的值.
,求a的值.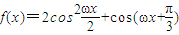 (ω>0)图象的两个相邻交点,且
(ω>0)图象的两个相邻交点,且 .
. 的面积为
的面积为 ,求a的值.
,求a的值.