题目内容
甲、乙两机床加工同一种零件,抽检得到它们加工后的零件尺寸x(单位:cm)及个数y如下表.| 1.01 | 1.02 | 1.03 | 1.04 | 1.05 | ||
| 零件尺寸x | 甲 | 3 | 7 | 8 | 9 | 3 |
| 零件个数y | 乙 | 7 | 4 | 4 | 4 | a |
(1)是否有99%的把握认为加工零件的质量与甲、乙有关?
(2)从甲、乙加工后尺寸大于1.03cm的零件中各取1个,求恰好取到2个都是不合格零件的概率.
【答案】分析:(1)根据所给的公式,代入数据求出临界值,把求得的结果同临界值表进行比较,看出有多大的把握认为加工零件的质量与甲、乙有关.
(2)尺寸大于1.03cm的零件中,甲有合格零件9个、不合格零件3个,乙有合格零件4个、不合格零件11个女.利用乘法原是得出可能的结果组成的基本事件个数,及满足条件事件数,求出概率.
解答:解:(1)根据题意得,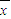 =1.03,
=1.03,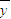 =
=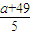 ,(1分)
,(1分)
由y=-91+100x知,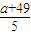 =-91+100×1.03,所以,a=11,(2分)
=-91+100×1.03,所以,a=11,(2分)
由于合格零件尺寸为1.03±0.01,故甲、乙加工的合格与不合格零件的数据表为:
(3分)
所以,K2=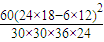 =10.(5分)
=10.(5分)
因K2=10>6.635,故有99%的把握认为加工的不合格零件与甲、乙有关联. (6分)
(2)尺寸大于1.03cm的零件中,甲有合格零件9个、不合格零件3个,乙有合格零件4个、不合格零件11个.(7分)
设甲加工的合格零件为A1,A2,…,A9,甲加工的不合格零件为A19,A11,A12,乙加工的合格零件为B1,B2,B3,B4,乙加工的不合格零件为B5,B6,…,B15.
因此,“从甲、乙中各取1个”的所有基本事件共12×15=180种情况.(9分)
其中,“取到的2个都是不合格零件”的基本事件共3×11=33种情况.(11分)
故所求概率为 =
=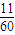 .(12分)
.(12分)
点评:本题是一个统计综合题,包含独立性检验和概率,本题通过创设情境激发学生学习数学的情感,帮助培养其严谨治学的态度.
(2)尺寸大于1.03cm的零件中,甲有合格零件9个、不合格零件3个,乙有合格零件4个、不合格零件11个女.利用乘法原是得出可能的结果组成的基本事件个数,及满足条件事件数,求出概率.
解答:解:(1)根据题意得,
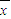 =1.03,
=1.03,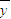 =
=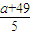 ,(1分)
,(1分)由y=-91+100x知,
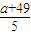 =-91+100×1.03,所以,a=11,(2分)
=-91+100×1.03,所以,a=11,(2分)由于合格零件尺寸为1.03±0.01,故甲、乙加工的合格与不合格零件的数据表为:
| 合格零件数 | 不合格零件数 | 合计 | |
| 甲 | 24 | 6 | 30 |
| 乙 | 12 | 18 | 30 |
| 合计 | 36 | 24 | 60 |
所以,K2=
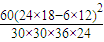 =10.(5分)
=10.(5分)因K2=10>6.635,故有99%的把握认为加工的不合格零件与甲、乙有关联. (6分)
(2)尺寸大于1.03cm的零件中,甲有合格零件9个、不合格零件3个,乙有合格零件4个、不合格零件11个.(7分)
设甲加工的合格零件为A1,A2,…,A9,甲加工的不合格零件为A19,A11,A12,乙加工的合格零件为B1,B2,B3,B4,乙加工的不合格零件为B5,B6,…,B15.
因此,“从甲、乙中各取1个”的所有基本事件共12×15=180种情况.(9分)
其中,“取到的2个都是不合格零件”的基本事件共3×11=33种情况.(11分)
故所求概率为
 =
=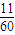 .(12分)
.(12分)点评:本题是一个统计综合题,包含独立性检验和概率,本题通过创设情境激发学生学习数学的情感,帮助培养其严谨治学的态度.

练习册系列答案
相关题目