题目内容
定义在R上的函数f(x)满足 ,且当0≤x1<x2≤1时,f(x1)≤f(x2).则
,且当0≤x1<x2≤1时,f(x1)≤f(x2).则 等于?
等于?
解:∵f(0)=0,f(x)+f(1-x)=1,令x=1得:f(1)=1,
又f( )=
)= f(x),
f(x),
∴当x=1时,f( )=
)= f(1)=
f(1)= ;
;
令x= ,由f(
,由f( )=
)= f(x)得:
f(x)得:
f( )=
)= f(
f( )=
)= ;
;
同理可求:f( )=
)= f(
f( )=
)= ;
;
f( )=)=
)=)= f(
f( )=
)= ;
;
f(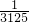 )=
)= f(
f( )=
)= ①
①
再令x= ,由f(x)+f(1-x)=1,可求得f(
,由f(x)+f(1-x)=1,可求得f( )=
)= ,
,
∴f( )+f(1-
)+f(1- )=1,解得f(
)=1,解得f( )=
)= ,
,
令x= ,同理反复利用f(
,同理反复利用f( )=
)= f(x),
f(x),
可得f( )=)=
)=)= f(
f( )=
)= ;
;
f(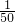 )=
)= f(
f( )=
)= ;
;
…
f( )=
)= f(
f(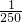 )=
)= ②
②
由①②可得:,有f( )=f(
)=f(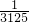 )=
)= ,
,
∵0≤x1<x2≤1时f(x1)≤f(x2),而0<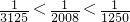 <1
<1
所以有f( )≥f(
)≥f(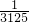 )=
)= ,
,
f( )≤f(
)≤f( )=
)= ;
;
故 =
= .
.
分析:可令x=1,由f(0)=0,f(x)+f(1-x)=1,求得f(1)=1,又f( )=
)= f(x)?f(
f(x)?f( )=
)= ;反复利用f(
;反复利用f( )=
)= f(x)?f(
f(x)?f(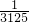 )=
)= f(
f( )=
)= ①;再令x=
①;再令x= ,由f(x)+f(1-x)=1,可求得f(
,由f(x)+f(1-x)=1,可求得f( )=
)= ,同理反复利用f(
,同理反复利用f( )=
)= f(x)?f(
f(x)?f( )=
)= f(
f(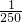 )=
)= ②;又0≤x1<x2≤1时f(x1)≤f(x2),而
②;又0≤x1<x2≤1时f(x1)≤f(x2),而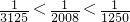 从而可求得f(
从而可求得f( )的值.
)的值.
点评:本题主要考查了抽象函数及其应用,解题的关键两次赋值后都反复应用f( )=
)= f(x),同时考查了计算能力,属于中档题.
f(x),同时考查了计算能力,属于中档题.
又f(
 )=
)= f(x),
f(x),∴当x=1时,f(
 )=
)= f(1)=
f(1)= ;
;令x=
 ,由f(
,由f( )=
)= f(x)得:
f(x)得:f(
 )=
)= f(
f( )=
)= ;
;同理可求:f(
 )=
)= f(
f( )=
)= ;
;f(
 )=)=
)=)= f(
f( )=
)= ;
;f(
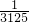 )=
)= f(
f( )=
)= ①
①再令x=
 ,由f(x)+f(1-x)=1,可求得f(
,由f(x)+f(1-x)=1,可求得f( )=
)= ,
,∴f(
 )+f(1-
)+f(1- )=1,解得f(
)=1,解得f( )=
)= ,
,令x=
 ,同理反复利用f(
,同理反复利用f( )=
)= f(x),
f(x),可得f(
 )=)=
)=)= f(
f( )=
)= ;
;f(
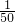 )=
)= f(
f( )=
)= ;
;…
f(
 )=
)= f(
f(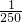 )=
)= ②
②由①②可得:,有f(
 )=f(
)=f(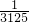 )=
)= ,
,∵0≤x1<x2≤1时f(x1)≤f(x2),而0<
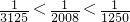 <1
<1所以有f(
 )≥f(
)≥f(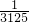 )=
)= ,
,f(
 )≤f(
)≤f( )=
)= ;
;故
 =
= .
.分析:可令x=1,由f(0)=0,f(x)+f(1-x)=1,求得f(1)=1,又f(
 )=
)= f(x)?f(
f(x)?f( )=
)= ;反复利用f(
;反复利用f( )=
)= f(x)?f(
f(x)?f(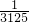 )=
)= f(
f( )=
)= ①;再令x=
①;再令x= ,由f(x)+f(1-x)=1,可求得f(
,由f(x)+f(1-x)=1,可求得f( )=
)= ,同理反复利用f(
,同理反复利用f( )=
)= f(x)?f(
f(x)?f( )=
)= f(
f(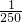 )=
)= ②;又0≤x1<x2≤1时f(x1)≤f(x2),而
②;又0≤x1<x2≤1时f(x1)≤f(x2),而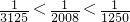 从而可求得f(
从而可求得f( )的值.
)的值.点评:本题主要考查了抽象函数及其应用,解题的关键两次赋值后都反复应用f(
 )=
)= f(x),同时考查了计算能力,属于中档题.
f(x),同时考查了计算能力,属于中档题. 
练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目