题目内容
设数列{an}的前n项和为Sn,对一切n∈N*,点(n,Sn)在函数f(x)=x2+x的图象上.(1)求an的表达式.
(2)将数列{an}依次按1项、2项、3项、4项循环地分为(a1),(a2,a3),(a4,a5,a6),(a7,a8,a9,a10);(a11),(a 12,a13),(a14,a15,a16),(a17,a18,a19,a20);(a21),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为{bn},求b5+b100的值.
(3)设An为数列{
}的前n项积,是否存在实数a,使得不等式An
＜a
对一切n∈N*都成立?若存在,求出a的取值范围;若不存在,请说明理由.
解:(1)因为点(n,Sn)在函数f(x)=x2+x的图象上,所以Sn=n2+n.
当n≥2时,an=Sn-Sn-1=n2+n-［(n-1)2+(n-1)］=2n.
当n=1时,a1=S1=2,满足an=2n.
所以an=2n(n∈N*).
(2)因为an=2n(n∈N*),所以数列{an}依次按1项、2项、3项、4项循环地分为(2),(4,6),(8,10,12),(14,16,18,20);(22),(24,26),(28,30,32),(34,36,38,40);(42),….将每一次循环记为一组.由于每一个循环含有4个括号,故b100是第25组中第4个括号内各数之和.
由分组规律知,由各组第4个括号中所有第1个数组成的数列是等差数列,且公差为20.
同理,由各组第4个括号中所有第2个数、所有第3个数、所有第4个数分别组成的数列也都是等差数列,且公差均为20.故各组第4个括号中各数之和构成等差数列,且公差为80.注意到第一组中第4个括号内各数之和是68,所以b100=68+24×80=1 988.
又b5=22,所以b5+b100=2 010.
(3)因为=1,
故An=(1)(1
)·…·(1
),
所以An
=(1
)(1
)·…·(1
)
.
又An
＜a
对一切n∈N*都成立,即
(1
)(1
)·…·(1
)2n+1＜a
对一切n∈N*都成立.
设g(n)=(1
)(1
)·…·(1
)2n+1,则只需［g(n)］max＜a
即可.
由于
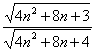=(1
)·
=
·
=
＜1,
所以g(n+1)＜g(n),故g(n)单调递减.
于是［g(n)］max=g(1)=
.
令
＜a
,即
＞0,解得
＜a＜0或a＞
.
综上所述,使得所给不等式对一切n∈N*都成立的实数a存在,a的取值范围是(
,0)∪(
,+∞).
