题目内容
已知数列an,其前n项和为 .
.(Ⅰ)求数列an的通项公式,并证明数列an是等差数列;
(Ⅱ)如果数列bn满足an=log2bn,请证明数列bn是等比数列,并求其前n项和;
(Ⅲ)设
 ,数列{cn}的前n项和为Tn,求使不等式Tn>
,数列{cn}的前n项和为Tn,求使不等式Tn> 对一切n∈N*都成立的最大正整数k的值.
对一切n∈N*都成立的最大正整数k的值.
【答案】分析:(Ⅰ)利用
(Ⅱ)用等比数列的定义证明 ;先判断公比是否为1,再选择等比数列的前 n 项和公式求解
;先判断公比是否为1,再选择等比数列的前 n 项和公式求解
(Ⅲ)裂项求和求Tn,判断Tn-Tn+1的正负,证明数列{Tn}的单调性,求出Tn的最值 ,解k
,解k
解答:解:(Ⅰ)当n=1时,a1=S1=5,(1分)
当n≥2时, =
= .(2分)
.(2分)
又a1=5满足an=3n+2,(3分)
∴an=3n+2?(n∈N*).(4分)
∵an-an-1=3n+2-[3(n-1)+2]=3(n≥2,n∈N*),
∴数列an是以5为首项,3为公差的等差数列.(5分)
(Ⅱ)由已知得 (n∈N*),(6分)
(n∈N*),(6分)
∵ (n∈N*),(7分)
(n∈N*),(7分)
又 ,
,
∴数列bn是以32为首项,8为公比的等比数列.(8分)
∴数列bn前n项和为 .(9分)
.(9分)
(Ⅲ) (10分)
(10分)
∴ =
= .(11分)
.(11分)
∵ (n∈N*),
(n∈N*),
∴Tn单调递增.
∴ .(12分)
.(12分)
∴ ,解得k<19,因为k是正整数,∴kmax=18.(13分)
,解得k<19,因为k是正整数,∴kmax=18.(13分)
点评:当已知条件中含有Sn,会用 ,由前n项和求通项公式,是高考对数列部分的考查的重点,本题综合考查由和求项、等差数列的证明,等比数列的求和公式,及裂项求和,把握好裂项相消后余下的项.
,由前n项和求通项公式,是高考对数列部分的考查的重点,本题综合考查由和求项、等差数列的证明,等比数列的求和公式,及裂项求和,把握好裂项相消后余下的项.

(Ⅱ)用等比数列的定义证明
 ;先判断公比是否为1,再选择等比数列的前 n 项和公式求解
;先判断公比是否为1,再选择等比数列的前 n 项和公式求解(Ⅲ)裂项求和求Tn,判断Tn-Tn+1的正负,证明数列{Tn}的单调性,求出Tn的最值
 ,解k
,解k解答:解:(Ⅰ)当n=1时,a1=S1=5,(1分)
当n≥2时,
 =
= .(2分)
.(2分)又a1=5满足an=3n+2,(3分)
∴an=3n+2?(n∈N*).(4分)
∵an-an-1=3n+2-[3(n-1)+2]=3(n≥2,n∈N*),
∴数列an是以5为首项,3为公差的等差数列.(5分)
(Ⅱ)由已知得
 (n∈N*),(6分)
(n∈N*),(6分)∵
 (n∈N*),(7分)
(n∈N*),(7分)又
 ,
,∴数列bn是以32为首项,8为公比的等比数列.(8分)
∴数列bn前n项和为
 .(9分)
.(9分)(Ⅲ)
 (10分)
(10分)∴
 =
= .(11分)
.(11分)∵
 (n∈N*),
(n∈N*),∴Tn单调递增.
∴
 .(12分)
.(12分)∴
 ,解得k<19,因为k是正整数,∴kmax=18.(13分)
,解得k<19,因为k是正整数,∴kmax=18.(13分)点评:当已知条件中含有Sn,会用
 ,由前n项和求通项公式,是高考对数列部分的考查的重点,本题综合考查由和求项、等差数列的证明,等比数列的求和公式,及裂项求和,把握好裂项相消后余下的项.
,由前n项和求通项公式,是高考对数列部分的考查的重点,本题综合考查由和求项、等差数列的证明,等比数列的求和公式,及裂项求和,把握好裂项相消后余下的项. 
练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
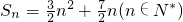 .
.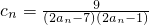 ,数列{cn}的前n项和为Tn,求使不等式Tn>
,数列{cn}的前n项和为Tn,求使不等式Tn>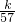 对一切n∈N*都成立的最大正整数k的值.
对一切n∈N*都成立的最大正整数k的值. .
. ,数列{cn}的前n项和为Tn,求使不等式Tn>
,数列{cn}的前n项和为Tn,求使不等式Tn> 对一切n∈N*都成立的最大正整数k的值.
对一切n∈N*都成立的最大正整数k的值.