题目内容
已知数列{an}的前n项和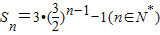 ,数列{bn}满足
,数列{bn}满足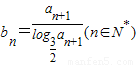 .
.(1)求数列{an}的通项公式,并说明{an}是否为等比数列;
(2)求数列
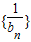 的前n项和前Tn;
的前n项和前Tn;(3)若-
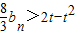 对任意的n∈N*恒成立,求t的最小正整数值.
对任意的n∈N*恒成立,求t的最小正整数值.
【答案】分析:(1)利用数列递推式,再写一式,两式相减可得数列通项,利用等比数列的定义可得结论;
(2)确定数列的通项,利用错位相减法求数列的和;
(3)确定bn的最小值为b2=b3= ,从而将不等式转化为t的不等式,即可求得结论.
,从而将不等式转化为t的不等式,即可求得结论.
解答:解:(1)当n=1时,a1=S1=3×1-1=2;
当n≥2时,an=Sn-Sn-1=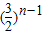
∴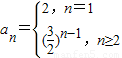
∵n=1时,a1=S1=3×1-1=2不满足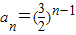
∴{an}不是等比数列;
(2)∵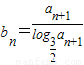 =
=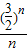 ,
,
∴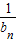 =
=
∴数列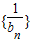 的前n项和前Tn=
的前n项和前Tn=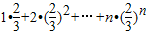
∴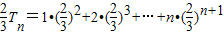
两式相减可得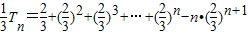 =
=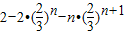
∴Tn=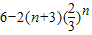
(3)由(2)有bn+1-bn=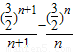 =
=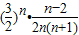
∴n≤2时,有bn+1-bn≤0;n>2时,bn+1-bn>0
∴bn的最小值为b2=b3=
∴-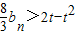 等价于-
等价于-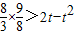
∴t2-2t-3>0
∴t>3或t<-1
∴t的最小正整数值是4.
点评:本题考查数列的通项与求和,考查恒成立问题,考查错位相减法的运用,考查学生分析解决问题的能力,属于中档题.
(2)确定数列的通项,利用错位相减法求数列的和;
(3)确定bn的最小值为b2=b3=
 ,从而将不等式转化为t的不等式,即可求得结论.
,从而将不等式转化为t的不等式,即可求得结论.解答:解:(1)当n=1时,a1=S1=3×1-1=2;
当n≥2时,an=Sn-Sn-1=
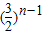
∴
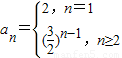
∵n=1时,a1=S1=3×1-1=2不满足
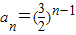
∴{an}不是等比数列;
(2)∵
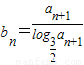 =
=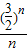 ,
,∴
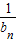 =
=
∴数列
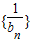 的前n项和前Tn=
的前n项和前Tn=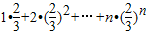
∴
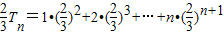
两式相减可得
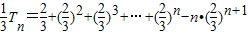 =
=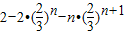
∴Tn=
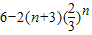
(3)由(2)有bn+1-bn=
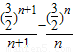 =
=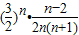
∴n≤2时,有bn+1-bn≤0;n>2时,bn+1-bn>0
∴bn的最小值为b2=b3=

∴-
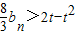 等价于-
等价于-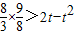
∴t2-2t-3>0
∴t>3或t<-1
∴t的最小正整数值是4.
点评:本题考查数列的通项与求和,考查恒成立问题,考查错位相减法的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |