题目内容
已知数列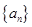 满足
满足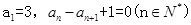 则此数列中
则此数列中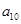 等于
等于
| A.-7 | B.11 | C.12 | D.-6 |
C
解析试题分析:根据题意,由于数列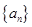 满足
满足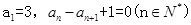 ,那么根据递推关系式可知,
,那么根据递推关系式可知, ,说明数列是公差为1,首项为3的等差数列,故可知通项公式为
,说明数列是公差为1,首项为3的等差数列,故可知通项公式为 ,故选C.
,故选C.
考点:等差数列的通项公式
点评:本题考查了等差数列的通项公式,考查了等差数列的概念,此题是基础题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
已知等比数列 的公比为q,记
的公比为q,记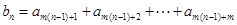 ,
,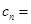
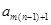 ·
·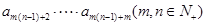 ,则以下结论一定正确的是( )
,则以下结论一定正确的是( )
A.数列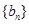 为等差数列,公差为 为等差数列,公差为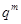 |
B.数列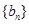 为等比数列,公比为 为等比数列,公比为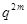 |
C.数列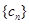 为等比数列,公比为 为等比数列,公比为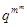 |
D.数列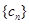 为等比数列,公比为 为等比数列,公比为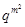 |
数列 满足
满足 并且
并且 ,则数列
,则数列 的第100项为( )
的第100项为( )
A. | B. | C. | D. |
已知等比数列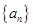 的首项
的首项 ,公比
,公比 ,等差数列
,等差数列 的首项
的首项 ,公差
,公差 ,在
,在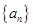 中插入
中插入 中的项后从小到大构成新数列
中的项后从小到大构成新数列 ,则
,则 的第100项为( )
的第100项为( )
| A.270 | B.273 | C.276 | D.279 |
已知数列 ,
, ,若该数列是递减数列,则实数
,若该数列是递减数列,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
数列{an}的通项公式 (
( ),若前n项的和
),若前n项的和 ,则项数n为
,则项数n为
A.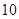 | B.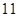 | C.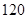 | D.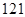 |
数列{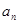 }的通项公式是
}的通项公式是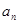 =
= (
( ),那么
),那么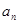 与
与 的大小关系是( )
的大小关系是( )
A.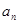 > > | B.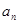 < < |
C.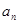 = =  | D.不能确定 |
已知数列 的通项公式为
的通项公式为 ,设其前
,设其前 项和为
项和为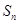 ,则使
,则使 成立的自然数
成立的自然数 有( )
有( )
| A.最大值31 | B.最小值31 | C.最大值63 | D.最小值63 |
 的首相
的首相 ,和递推关系
,和递推关系 (
( 且
且 ),探求其通项公式为____________.
),探求其通项公式为____________.