题目内容
在棱长为2的正方体ABCD—A1B1C1D1中,E、F、H分别为BB1、DC、CC1的中点.(1)求证:D1F⊥平面DEH;
(2)求点D1到平面DEH的距离.
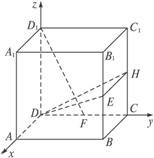
思路解析:本题所涉及的几何体是正方体,因此可以考虑通过建立直角坐标系来解决相应的问题.要证明线面垂直,围绕着线面垂直的判定定理,先证明线线垂直,转而证明相关的向量垂直,从而得出结论;再利用向量的相关知识求得点到面的距离.
解:如图所示建立空间直角坐标系,则点D(0,0,0),B(2,2,0),C(0,2,0),B1(2,2,2),C1(0,2,2),D1(0,0,2),E(2,2,1),F(0,1,0),H(0,2,1).
(1)![]() =(2,0,0),
=(2,0,0),![]() =(0,2,1),
=(0,2,1),![]() =(0,-1,2),
=(0,-1,2),![]() =2×0+(-1)×0+2×0=0,
=2×0+(-1)×0+2×0=0,![]() ⊥
⊥![]() ,同理,
,同理,![]() ⊥
⊥![]() ,∴
,∴![]() ⊥平面DEH.
⊥平面DEH.
(2)由(1)知,D1F⊥平面DEH,所以![]() =(0,-1,2)是平面DEH的一个法向量,因此点D1到平面DEH的距离是d=
=(0,-1,2)是平面DEH的一个法向量,因此点D1到平面DEH的距离是d=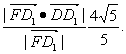

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在棱长为2的正方体AC1中,G是AA1的中点,则BD到平面GB1D1的距离是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在棱长为2的正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1、AD的中点,那么异面直线OE和FD1所成的角的余弦值等于( )
如图,在棱长为2的正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1、AD的中点,那么异面直线OE和FD1所成的角的余弦值等于( ) (理科)如图,在棱长为1的正方体A'C中,过BD及B'C'的中点E作截面BEFD交C'D'于F.
(理科)如图,在棱长为1的正方体A'C中,过BD及B'C'的中点E作截面BEFD交C'D'于F. (2007•上海)如图,在棱长为2的正方体ABCD-A'B'C'D'中,E,F分别是A'B'和AB的中点,求异面直线A'F与CE所成角的大小 (结果用反三角函数值表示).
(2007•上海)如图,在棱长为2的正方体ABCD-A'B'C'D'中,E,F分别是A'B'和AB的中点,求异面直线A'F与CE所成角的大小 (结果用反三角函数值表示).