题目内容
如图，在梯形ABCD中，AD∥BC，AB⊥BC，AB=BC=1，PA⊥平面ABCD，CD⊥PC．
（Ⅰ）证明：CD⊥平面PAC；
（Ⅱ）若E为AD的中点，求证：CE∥平面PAB．
（Ⅰ）证明：CD⊥平面PAC；
（Ⅱ）若E为AD的中点，求证：CE∥平面PAB．
（Ⅰ）证明：∵PA⊥平面ABCD，CD?平面ABCD
∴CD⊥PA…（2分）
又∵CD⊥PC…（3分）
而PC∩PA=P…（4分）
所以，CD⊥面PAC…（5分）
（Ⅱ）∵AB⊥BC，AB=BC=1
∴∠BAC=45°∴∠CAD=45°…（6分）
又由（Ⅰ）CD⊥面PAC
∴CD⊥AC
∴△ACD为等腰直角三角形 …（7分）
又E为AD中点∴CE⊥AD…（8分）
又∵BC∥AD∴CE⊥BC
所以，∴CE∥AB…（9分）
而AB?面PAB，CE?面PAB
所以CE∥面PAB…（10分）
∴CD⊥PA…（2分）
又∵CD⊥PC…（3分）
而PC∩PA=P…（4分）
所以，CD⊥面PAC…（5分）
（Ⅱ）∵AB⊥BC，AB=BC=1
∴∠BAC=45°∴∠CAD=45°…（6分）
又由（Ⅰ）CD⊥面PAC
∴CD⊥AC
∴△ACD为等腰直角三角形 …（7分）
又E为AD中点∴CE⊥AD…（8分）
又∵BC∥AD∴CE⊥BC
所以，∴CE∥AB…（9分）
而AB?面PAB，CE?面PAB
所以CE∥面PAB…（10分）
练习册系列答案
名校名卷单元同步训练测试题系列答案
相关题目
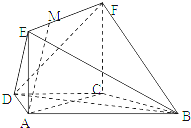如图，在梯形ABCD中，AB∥CD，AD=DC=CB=a，．∠ABC=60°，平面ACFE⊥平面ABCD，四边形ACFE是矩形，AE=a，点M在线段EF上．
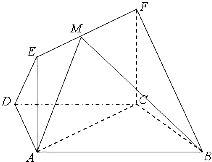如图，在梯形ABCD中，AB∥CD，AD=DC=CB=1，∠ABC=60°，四边形ACFE为矩形，平面ACFE⊥平面ABCD，CF=1．
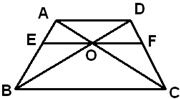如图，在梯形ABCD中，AD∥BC，BD与AC相交于O，过O的直线分别交AB、CD于E、F，且EF∥BC，若AD=12，BC=20，则EF=
如图，在梯形ABCD中，对角线AC和BD交于点O，E、F分别是AC和BD的中点，分别写出
如图，在梯形△ABCD中，AB∥CD，AD=DC-=CB=1，么ABC-60．，四边形ACFE为矩形，平面ACFE上平面ABCD，CF=1．