题目内容
已知函数f(x)的图象与函数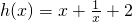 的图象关于点A(0,1)对称,若
的图象关于点A(0,1)对称,若 ,且g(x)在区间(0,2]上为减函数,则实数a的取值范围是
,且g(x)在区间(0,2]上为减函数,则实数a的取值范围是
- A.[3,+∞)
- B.[2,+∞)
- C.(0,3]
- D.(0,2]
A
分析:利用函数图象对称的公式,求得f(x)=2-h(-x)= ,由此可得g(x)=x+
,由此可得g(x)=x+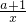 .然后对函数g(x)求导数,并讨论导数g'(x)在区间(0,2]恒小于或等于0,即可得到实数a的取值范围.
.然后对函数g(x)求导数,并讨论导数g'(x)在区间(0,2]恒小于或等于0,即可得到实数a的取值范围.
解答:∵函数f(x)的图象与函数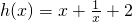 的图象关于点A(0,1)对称,
的图象关于点A(0,1)对称,
∴f(x)=2-h(-x)=2-( )=
)=
由此可得 =x+
=x+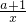 ,对g(x)求导数,得g'(x)=1-
,对g(x)求导数,得g'(x)=1-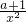
∵g(x)在区间(0,2]上为减函数,
∴g'(x)=1-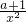 ≤0在区间(0,2]恒成立,即
≤0在区间(0,2]恒成立,即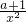 ≥1,可得x2≤a+1
≥1,可得x2≤a+1
∴x2的最大值小于或等于a+1,即a+1≥4,a≥3
故选A
点评:本题用导数为工具讨论函数的单调性,着重考查了函数的单调性、函数图象的对称性质和不等式恒成立的讨论等知识,属于基础题.
分析:利用函数图象对称的公式,求得f(x)=2-h(-x)=
 ,由此可得g(x)=x+
,由此可得g(x)=x+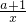 .然后对函数g(x)求导数,并讨论导数g'(x)在区间(0,2]恒小于或等于0,即可得到实数a的取值范围.
.然后对函数g(x)求导数,并讨论导数g'(x)在区间(0,2]恒小于或等于0,即可得到实数a的取值范围.解答:∵函数f(x)的图象与函数
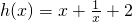 的图象关于点A(0,1)对称,
的图象关于点A(0,1)对称,∴f(x)=2-h(-x)=2-(
 )=
)=
由此可得
 =x+
=x+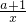 ,对g(x)求导数,得g'(x)=1-
,对g(x)求导数,得g'(x)=1-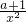
∵g(x)在区间(0,2]上为减函数,
∴g'(x)=1-
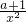 ≤0在区间(0,2]恒成立,即
≤0在区间(0,2]恒成立,即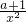 ≥1,可得x2≤a+1
≥1,可得x2≤a+1∴x2的最大值小于或等于a+1,即a+1≥4,a≥3
故选A
点评:本题用导数为工具讨论函数的单调性,着重考查了函数的单调性、函数图象的对称性质和不等式恒成立的讨论等知识,属于基础题.

练习册系列答案
相关题目
已知函数f(x)的图象关于直线x=2对称,且当x≠2时其导函数f′(x)满足xf′(x)>2f′(x),若2<a<4,则下列表示大小关系的式子正确的是( )
| A、f(2a)<f(3)<f(log2a) | B、f(3)<f(log2a)<f(2a) | C、f(log2a)<f(3)<f(2a) | D、f(log2a)<f(2a)<f(3) |
 (2011•焦作一模)已知函数f(x)的图象过点(
(2011•焦作一模)已知函数f(x)的图象过点(