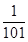题目内容
设首项为1的数列{an}的前n项和为Sn,且Sn+1-2Sn=2n,n∈N*,则其通项an=________.
(n+1)2n-2
分析:利用Sn-Sn-1=an,转化Sn+1-2Sn=2n,为Sn=an+1-2n的关系,推出an+1=2an+2 n-1,说明{ }是以
}是以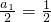 为首相d=
为首相d= 为公差的等差数列,即可求出通项公式.
为公差的等差数列,即可求出通项公式.
解答:由Sn-Sn-1=an则Sn+1-Sn=an+1,
Sn+1-2Sn=2n,n∈N*,
Sn+1-Sn-Sn=2n,
则an+1-Sn=2n,
Sn=an+1-2n,
∴an=Sn-Sn-1
=an+1-2n-[an-2n-1]
=-2 n-1+an+1-an
∴an+1=2an+2 n-1(两边同除以2n+1)
∴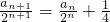 ,
,
∴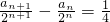 ,
,
所以{ }是以
}是以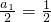 为首相d=
为首相d= 为公差的等差数列
为公差的等差数列
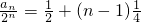
化简:an=(n+1)2n-2.
故答案为:(n+1)2n-2.
点评:本题是中档题,考查数列递推关系式的应用,数列通项公式的求法,把数列转化为等差数列是解题的关键,考查转化思想,计算能力.
分析:利用Sn-Sn-1=an,转化Sn+1-2Sn=2n,为Sn=an+1-2n的关系,推出an+1=2an+2 n-1,说明{
 }是以
}是以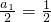 为首相d=
为首相d= 为公差的等差数列,即可求出通项公式.
为公差的等差数列,即可求出通项公式.解答:由Sn-Sn-1=an则Sn+1-Sn=an+1,
Sn+1-2Sn=2n,n∈N*,
Sn+1-Sn-Sn=2n,
则an+1-Sn=2n,
Sn=an+1-2n,
∴an=Sn-Sn-1
=an+1-2n-[an-2n-1]
=-2 n-1+an+1-an
∴an+1=2an+2 n-1(两边同除以2n+1)
∴
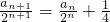 ,
,∴
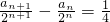 ,
,所以{
 }是以
}是以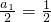 为首相d=
为首相d= 为公差的等差数列
为公差的等差数列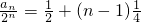
化简:an=(n+1)2n-2.
故答案为:(n+1)2n-2.
点评:本题是中档题,考查数列递推关系式的应用,数列通项公式的求法,把数列转化为等差数列是解题的关键,考查转化思想,计算能力.

练习册系列答案
相关题目

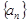 是首项为1的正项数列,且
是首项为1的正项数列,且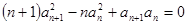 (
(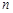 =1,2,3,…),则它的通项公式是
=1,2,3,…),则它的通项公式是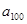 =( ).
=( ). 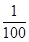 C. 101
D.
C. 101
D.