Question

（本小题满分14分）

       在平面直角坐标系xOy上，给定抛物线L:_．实数p，q满足，x₁，x₂是方程的两根，记。

（1）过点作L的切线教y轴于点       B．证明：对线段AB上任一点Q（p，q）有

（2）设M（a，b）是定点，其中a，b满足a²-4b>0,a≠0．过M（a，b）作L的两条切线，切点分别为，与y轴分别交与F,F'。线段EF上异于两端点的点集记为X．证明：M（a,b） X_;

（3）设D={ （x,y）|y≤x-1,y≥（x+1）²-}．当点（p,q）取遍D时，求的最小值 （记为）和最大值（记为）．

Answer 1

（本小题满分14分）

       解：（1）证明：切线的方程为

      

       当

       当

   （2）的方程分别为

       求得的坐标，由于，故有

       1）先证：

       （）设

       当

       当

       （）设

       当

       注意到

       2）次证：

   （）已知利用（1）有

   （）设，断言必有

       若不然，令Y是上线段上异于两端点的点的集合，

       由已证的等价式1）再由（1）得，矛盾。

       故必有再由等价式1），

       综上，

   （3）求得的交点

       而是Ｌ的切点为的切线，且与轴交于，

       由（１）线段Q₁Q₂，有

       当

      

       在（0，2）上，令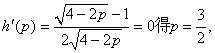

       由于

       在[0，2]上取得最大值

      

       故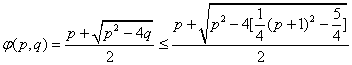      

      

      

       ,

       故