题目内容
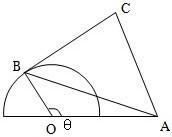
如图,半圆O的直径为2,A为直径的延长线上的一点,OA=2,B为半圆周上的动点,以AB为边,向形外作等边△ABC,问B点在什么位置时,四边形OACB的面积最大?并求出这个最大面积.
思路分析:本题主要综合考查正、余弦定理及函数的最值等问题,首先应建立四边形AOBC面积的函数关系式,然后讨论最值.
解:设∠AOB=x,由OA=2,OB=1.
知AB2=OA2+OB2-2OA·OBcosx=5-4cosx.
△ABC与△AOB的面积分别为
S△ABC=![]() AB2=
AB2=![]() (5-4cosx),
(5-4cosx),
S△AOB=![]() OA·OBsinx=sinx.
OA·OBsinx=sinx.
所以四边形OACB的面积为
S=![]() (5-4cosx)+sinx,
(5-4cosx)+sinx,
整理得S=![]() +2sin(x-60°).
+2sin(x-60°).
由上式可知,当x-60°=90°,即x=150°时,四边形OACB的面积最大,且其最大面积为![]() +2.
+2.

练习册系列答案
相关题目
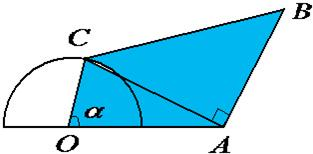 如图,半圆O的直径为2,A为直径延长线上一点,且OA=2,C为半圆上任意一点,以AC为直角边作等腰直角△ABC,求四边形OABC的面积最大值.
如图,半圆O的直径为2,A为直径延长线上一点,且OA=2,C为半圆上任意一点,以AC为直角边作等腰直角△ABC,求四边形OABC的面积最大值.
