题目内容
证明在△ABC中,a,b,c成等差数列的充要条件是acos2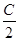
+ccos2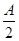 =
=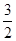 b.
b.
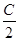
+ccos2
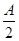 =
=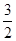 b.
b.见解析
在△ABC中,acos2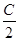 +c·cos2
+c·cos2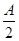 =
= ?
?
?a(1+cos C)+c(1+cos A)=3b?a+c+acos C+ccos A=3b
?a+c+a =3b?a+c+
=3b?a+c+ =3b
=3b
?a+c+b=3b?a+c=2b?a,b,c成等差数列.所以命题成立.
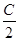 +c·cos2
+c·cos2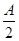 =
= ?
?
?a(1+cos C)+c(1+cos A)=3b?a+c+acos C+ccos A=3b
?a+c+a
 =3b?a+c+
=3b?a+c+ =3b
=3b?a+c+b=3b?a+c=2b?a,b,c成等差数列.所以命题成立.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
 ;
; ,若
,若 是
是 的必
的必 的取值范围.
的取值范围.  ”是“函数
”是“函数 为奇函数”的( )
为奇函数”的( ) ”的________条件.
”的________条件. ”是“函数
”是“函数 在区间
在区间 上单调递减”的( )
上单调递减”的( ) ,
, ,则
,则 是
是 成立的 ( )
成立的 ( ) 中,角
中,角 成等差数列是
成等差数列是 成立的
成立的