题目内容
数列{an}满足 ,
, .
.
(1)求数列{an}的通项公式;
(2)设ln(1+x)<x在x>0时成立,数列{an}的前n项和为Sn,证明 .
.
解:(1)∵ ,
, ,
,
∴ =
= ,
,
∴ =-1+
=-1+ ,
,
∴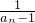 是首项为-2,公差为-1的等差数列.
是首项为-2,公差为-1的等差数列.
∴ ,所以
,所以 .
.
数列{an}的通项公式为 .
.
(2)∵ln(1+x)<x在x>0时成立,
从而ln(1+ )
) ,
, ln(1+
ln(1+ ),
),
∴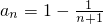 <1-ln(n+2)+ln(n+1),
<1-ln(n+2)+ln(n+1),
Sn<(1-ln3+ln2)+(1-ln4+ln3)+…+[1-ln(n+2)+ln(n+1)]=n+ln(n+2)-ln2=n-ln(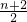 )
)
∴
分析:(1)利用已知条件,推出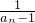 是首项为-2,公差为-1的等差数列.求出通项公式,然后求解即可.
是首项为-2,公差为-1的等差数列.求出通项公式,然后求解即可.
(2)利用ln(1+x)<x在x>0时成立,推出数列an<1-ln(n+2)+ln(n+1),的关系式,通过数列消项求和,推出结果.
点评:本题考查数列通项公式的求法,数列前n项和的求法,数列与不等式的综合应用,考查转化思想、计算能力.
 ,
, ,
,∴
 =
= ,
,∴
 =-1+
=-1+ ,
,∴
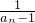 是首项为-2,公差为-1的等差数列.
是首项为-2,公差为-1的等差数列.∴
 ,所以
,所以 .
.数列{an}的通项公式为
 .
.(2)∵ln(1+x)<x在x>0时成立,
从而ln(1+
 )
) ,
, ln(1+
ln(1+ ),
),∴
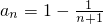 <1-ln(n+2)+ln(n+1),
<1-ln(n+2)+ln(n+1),Sn<(1-ln3+ln2)+(1-ln4+ln3)+…+[1-ln(n+2)+ln(n+1)]=n+ln(n+2)-ln2=n-ln(
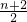 )
)∴

分析:(1)利用已知条件,推出
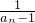 是首项为-2,公差为-1的等差数列.求出通项公式,然后求解即可.
是首项为-2,公差为-1的等差数列.求出通项公式,然后求解即可.(2)利用ln(1+x)<x在x>0时成立,推出数列an<1-ln(n+2)+ln(n+1),的关系式,通过数列消项求和,推出结果.
点评:本题考查数列通项公式的求法,数列前n项和的求法,数列与不等式的综合应用,考查转化思想、计算能力.

练习册系列答案
相关题目