题目内容
计算
(a≥1).
解:原式=
=
=|
+1|+|
－1|
=
=
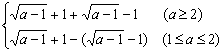
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
为了求1+2+22+23+…+22008的值，可令S=1=2+22+23+…+22008，则2S=2+22+23+24+…+22009，因此2S-S=22009-1，所以1+2+22+23+…+22008=22009-1仿照以上推理计算出1+5+52+53+…+52009的值是（ ）
| A、52009-1 | ||
| B、52010-1 | ||
| C、52009-1 | ||
D、
|
=