题目内容
已知数列{an}的前n项和Sn=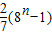 .
.(I)求数列{an}的通项公式an;
(II)设bn=log2an,求
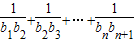 .
.
【答案】分析:(Ⅰ)由数列{an}的前n项和Sn=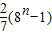 .利用公式an=
.利用公式an=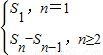 ,能求出数列{an}的通项公式an.
,能求出数列{an}的通项公式an.
(Ⅱ)由an=23n-2(n∈N*),知bn=log223n-2=3n-2,由此能求出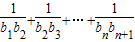 .
.
解答:解:(Ⅰ)a1=S1= (81-1)=2.…(1分)
(81-1)=2.…(1分)
当n≥2时,an=Sn-Sn-1
= (8n-1)-
(8n-1)- (8n-1-1)=23n-2.
(8n-1-1)=23n-2.
当n=1时上式也成立,
所以an=23n-2(n∈N*).…(6分)
(Ⅱ)由(Ⅰ)知,
bn=log223n-2=3n-2,…(7分)
所以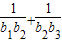 +…+
+…+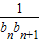
=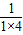 +
+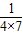 +…+
+…+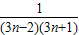
= [(1-
[(1- )+(
)+( -
- )+…+(
)+…+(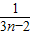 -
-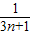 )]
)]
= (1-
(1-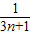 )
)
=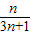 .…(12分)
.…(12分)
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法.解题时要认真审题,仔细解答,注意裂项求和法的合理运用.
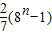 .利用公式an=
.利用公式an=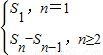 ,能求出数列{an}的通项公式an.
,能求出数列{an}的通项公式an.(Ⅱ)由an=23n-2(n∈N*),知bn=log223n-2=3n-2,由此能求出
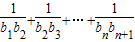 .
.解答:解:(Ⅰ)a1=S1=
 (81-1)=2.…(1分)
(81-1)=2.…(1分)当n≥2时,an=Sn-Sn-1
=
 (8n-1)-
(8n-1)- (8n-1-1)=23n-2.
(8n-1-1)=23n-2.当n=1时上式也成立,
所以an=23n-2(n∈N*).…(6分)
(Ⅱ)由(Ⅰ)知,
bn=log223n-2=3n-2,…(7分)
所以
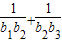 +…+
+…+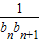
=
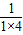 +
+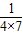 +…+
+…+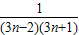
=
 [(1-
[(1- )+(
)+( -
- )+…+(
)+…+(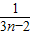 -
-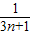 )]
)]=
 (1-
(1-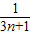 )
)=
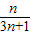 .…(12分)
.…(12分)点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法.解题时要认真审题,仔细解答,注意裂项求和法的合理运用.

练习册系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |