题目内容
| ∫ | 1-1 |
| 1-x2 |
∵
(1+
)dx=
1dx
dx
dx表示的几何意义是:
以(0,0)为圆心,1为半径第一,二象限内圆弧与坐标轴围成的面积
的一半,∴
dx=
×π×12=
,
又
1dx=x
=1-(-1)=2,
∴
(1+
)dx=
1dx
dx=2+
=
,
故答案为:
;
| ∫ | 1-1 |
| 1-x2 |
| ∫ | 1-1 |
| +∫ | 1-1 |
| 1-x2 |
| ∫ | 1-1 |
| 1-x2 |
以(0,0)为圆心,1为半径第一,二象限内圆弧与坐标轴围成的面积
的一半,∴
| ∫ | 1-1 |
| 1-x2 |
| 1 |
| 2 |
| π |
| 2 |
又
| ∫ | 1-1 |
| | | 1-1 |
∴
| ∫ | 1-1 |
| 1-x2 |
| ∫ | 1-1 |
| +∫ | 1-1 |
| 1-x2 |
| π |
| 2 |
| 4+π |
| 2 |
故答案为:
| 4+π |
| 2 |

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
已知函数f(
-1)=-x,则函数f(x)的表达式为( )
| x |
| A、f(x)=x2+2x+1(x≥0) |
| B、f(x)=x2+2x+1(x≥-1) |
| C、f(x)=-x2-2x-1(x≥0) |
| D、f(x)=-x2-2x-1(x≥-1) |
 .
.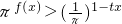 在t∈[-2,2]时恒成立,求实数x的取值范围.
在t∈[-2,2]时恒成立,求实数x的取值范围.