题目内容
1.已知M(3,y0)(y0>0)为抛物线C:y2=2px(p>0)上一点,F为抛物线C的焦点,且|MF|=5.(1)求抛物线C方程;
(2)MF的延长线交抛物线于另一点N,求N的坐标.
分析 (1)利用|MF|=3+$\frac{p}{2}$=5,计算即得结论;
(2)通过设MF所在直线的方程,并与抛物线C的方程联立,利用韦达定理计算即得结论.
解答  解:(1)∵|MF|=3+$\frac{p}{2}$=5,∴p=4,
解:(1)∵|MF|=3+$\frac{p}{2}$=5,∴p=4,
∴抛物线C方程为:y2=8x;
(2)∵MF不垂直于x轴,故可设MF所在直线的方程为:y=k(x-2),
与抛物线C的方程联立,可得:k2x2-(4k2+8)x+4k2=0,
由韦达定理可知:xMxN=$\frac{4{k}^{2}}{{k}^{2}}$=4,
∵xM=3,∴xN=$\frac{4}{3}$,
∵N为MF的延长线与抛物线的交点,
由图象可知yN<0,
∴yN=-$\sqrt{2p{x}_{N}}$=-$\frac{4\sqrt{6}}{3}$,
∴N($\frac{4}{3}$,-$\frac{4\sqrt{6}}{3}$).
点评 本题考查求抛物线的方程、求点的坐标,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
4.若α≠$\frac{kπ}{2}$(k∈Z),则f(α)=$\frac{sinα+tanα}{cosα+cotα}$的取值情况是( )
| A. | 必取正值 | B. | 必取负值 | C. | 可取零值 | D. | 可正可负 |
10.某几何体的三视图如图所示,则该几何体的体积为( )
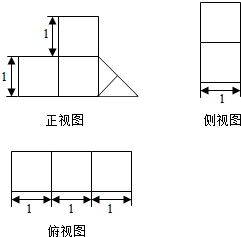

| A. | $\frac{7}{3}$ | B. | $\frac{7}{2}$ | C. | $\frac{9}{2}$ | D. | $\frac{9}{4}$ |