题目内容
【题目】[选修4—5：参数方程选讲]
在直角坐标系xoy中，曲线
的参数方程是
（t是参数），以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线
的极坐标方程是
(1)求曲线的普通方程和曲线的直角坐标方程；
(2)若两曲线交点为A、B，求
【答案】（1）
的普通方程是:
,曲线
的直角坐标方程是：
（2）
【解析】
（1）将C1的参数方程两边平分再相减消去参数t得到普通方程，将C2的极坐标方程展开，根据极坐标与直角坐标的对应关系得出C2的直角坐标方程；
（2）求出C2的参数方程，代入C1的普通方程，根据参数的几何意义得出交点间的距离．
（1）曲线的普通方程是:
曲线的直角坐标方程是：
(2)因为是过点
的直线
所以的的参数方程为：
（t为参数）
代入的的普通方程，得
解得
，故
阅读快车系列答案
【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验，并获得了煤气开关旋钮旋转的弧度数
与烧开一壶水所用时间
的一组数据，且作了一定的数据处理（如下表），得到了散点图（如下图）.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中
，
.
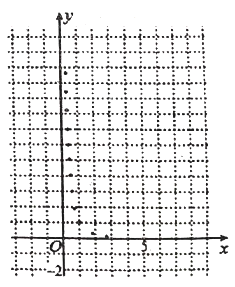
（1）根据散点图判断，
与
哪一个更适宜作烧水时间关于开关旋钮旋转的弧度数的回归方程类型？（不必说明理由）
（2）根据判断结果和表中数据，建立关于的回归方程；
（3）若单位时间内煤气输出量
与旋转的弧度数成正比，那么，利用第（2）问求得的回归方程知为多少时，烧开一壶水最省煤气？
附：对于一组数据
，其回归直线
的斜率和截距的最小二乘法估计值分别为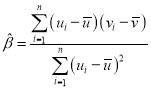
，
【题目】众所周知，城市公交车的数量太多会造成资源的浪费，太少又难以满足乘客的需求，为此，某市公交公司在某站台的50名候车乘客中随机抽取10名，统计了他们的候车时间（单位：分钟），得到下表.
候车时间 | 人数 |
| 1 |
| 4 |
| 2 |
| 2 |
| 1 |
（1）估计这10名乘客的平均候车时间（同一组中的每个数据可用该组区间的中点值代替）；
（2）估计这50名乘客的候车时间少于10分钟的人数.