题目内容
函数y=
的定义域是
- A.[2，+∞）
- B.（-∞，2]
- C.（-∞，-2）
- D.（2，+∞）
D
分析：对数的真数大于0，就是x-3＞0，直接求，解即可求出函数的定义域．
解答：函数y=
（2x-4）有意义
必须2x-4＞0
即：x＞2
故答案为：{x|x＞2}
点评：本题考查对数函数的定义域，考查学生发现问题解决问题的能力，本题关键是知道对数的真数大于0，是基础题．
分析：对数的真数大于0，就是x-3＞0，直接求，解即可求出函数的定义域．
解答：函数y=
（2x-4）有意义必须2x-4＞0
即：x＞2
故答案为：{x|x＞2}
点评：本题考查对数函数的定义域，考查学生发现问题解决问题的能力，本题关键是知道对数的真数大于0，是基础题．
练习册系列答案
相关题目
的定义域是( )
,(2k+1)π］（k∈Z） B.［2kπ+
,(2k+1)π］（k∈Z）
,(k+1)π］（k∈Z） D.［2kπ,(2k+1)π］（k∈Z）
的定义域是( )
的定义域是( ) 
或x≤1-
B.-1＜x＜3
≤x＜3或-1＜x≤1-
D.1-
≤x≤1+
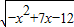的定义域是A，函数y=
（a＞0）在[0，2]上的值域为B．若A⊆B，求实数a的取值范围．
的定义域是 
B.（1，2） C.（2，+∞） D.(-∞,2)