题目内容
已知点P在椭圆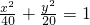 上,F1,F2是椭圆的两个焦点,△F1PF2是直角三角形,则这样的点P有
上,F1,F2是椭圆的两个焦点,△F1PF2是直角三角形,则这样的点P有
- A.2个
- B.4个
- C.6个
- D.8个
A
分析:如图,设椭圆的一个顶点是A,在三角形OAF1中,求得∠AOF2=45°,从而∠F1AF2=90°,根据当点P位于A(0,b)或(0,-b)处时,∠F1PF2最大.得到使得△F1PF2是直角三角形,则这样的点P有多少个即可.
解答: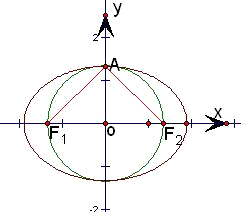 解:如图,设椭圆的一个顶点是A,
解:如图,设椭圆的一个顶点是A,
在三角形OAF1中,OA= ,AF2=
,AF2=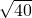 ,
,
∴cos∠AOF2= ,
,
∴∠AOF2=45°,
∴∠F1AF2=90°,
由图可知,,△F1PF2是直角三角形,则这样的点P有两个(即下下两个顶点)
故选A.
点评:本题考查椭圆的性质及其应用,难度不大,正确解题的关键是知道当点P位于A(0,b)或(0,-b)处时,∠F1PF2最大.
分析:如图,设椭圆的一个顶点是A,在三角形OAF1中,求得∠AOF2=45°,从而∠F1AF2=90°,根据当点P位于A(0,b)或(0,-b)处时,∠F1PF2最大.得到使得△F1PF2是直角三角形,则这样的点P有多少个即可.
解答:
 解:如图,设椭圆的一个顶点是A,
解:如图,设椭圆的一个顶点是A,在三角形OAF1中,OA=
 ,AF2=
,AF2=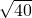 ,
,∴cos∠AOF2=
 ,
,∴∠AOF2=45°,
∴∠F1AF2=90°,
由图可知,,△F1PF2是直角三角形,则这样的点P有两个(即下下两个顶点)
故选A.
点评:本题考查椭圆的性质及其应用,难度不大,正确解题的关键是知道当点P位于A(0,b)或(0,-b)处时,∠F1PF2最大.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
 =1(a>b>0)上,以M为圆心的圆与x轴相切于椭圆的右焦点,若圆M与y轴相交于A,B两点,且△ABM是边长为
=1(a>b>0)上,以M为圆心的圆与x轴相切于椭圆的右焦点,若圆M与y轴相交于A,B两点,且△ABM是边长为 的正三角形.
的正三角形.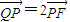 ,求直线l的斜率;
,求直线l的斜率; 左半部分交于H,K两点,又过椭圆N的右焦点F1做平行于HK的直线交椭圆N于R,S两点,试判断满足|GH|•|GK|=3|RF1|•|F1S|的直线GK是否存在?请说明理由.
左半部分交于H,K两点,又过椭圆N的右焦点F1做平行于HK的直线交椭圆N于R,S两点,试判断满足|GH|•|GK|=3|RF1|•|F1S|的直线GK是否存在?请说明理由.