题目内容
若点P为△ABC的外心，且
+
=
，则∠ACB的大小是（ ）
| PA |
| PB |
| PC |
分析：由题意可知外心P应在三角形的外部，知△ABC为钝角三角形，且PA=PB=PC，由向量加法的平行四边形法则，可知（AB的中点为M）
+
=2
，结合已知 且
+
=
，可得APBC是菱形，即可得出答案．
| PA |
| PB |
| PM |
| PA |
| PB |
| PC |
解答：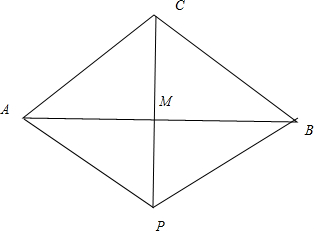
解：由
+
=
，可知△ABC为钝角三角形，外心P应在三角形的外部，且PA=PB=PC，
如图．
设AB的中点为M，则
+
=2
，又
+
=
，
∴2
=
，即P，C，M三点共线，且M是PC的中点，
∴APBC是菱形，
由可得∠ACP=∠BCP=60°，
∴∠ACB=120°，
故选C．
解：由| PA |
| PB |
| PC |
如图．
设AB的中点为M，则
| PA |
| PB |
| PM |
| PA |
| PB |
| PC |
∴2
| PM |
| PC |
∴APBC是菱形，
由可得∠ACP=∠BCP=60°，
∴∠ACB=120°，
故选C．
点评：本题主要考查了向量的加法的平行四边形法则的应用，向量共线定理的应用，解题的关键是熟练掌握向量的基本知识并能灵活应用．
练习册系列答案
相关题目