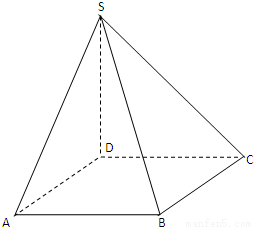
题目内容
如图，SD垂直于正方形ABCD所在的平面，AB=1，SB=
．
（1）求证：BC⊥SC；
（2）设棱SA的中点为M，求异面直线DM与SC所成角的大小．
| 3 |
（1）求证：BC⊥SC；
（2）设棱SA的中点为M，求异面直线DM与SC所成角的大小．
（1）证明：
?
?BC⊥平面SDC
所以，BC⊥SC
（2）取SB，CD，BC的中点分别为P，Q，R，连接MP，PQ，QR，PR
则PM
AB
DR?DM∥PQ，又PR
SC
所以∠RPQ为异面直线DM，SC所成角或其补角
计算易得∠RPQ=60°，即异面直线DM，SC所成角为60°
|
|
所以，BC⊥SC
（2）取SB，CD，BC的中点分别为P，Q，R，连接MP，PQ，QR，PR
则PM
| ||
| . |
| 1 |
| 2 |
| ||
| . |
| ||
| . |
| 1 |
| 2 |
所以∠RPQ为异面直线DM，SC所成角或其补角
计算易得∠RPQ=60°，即异面直线DM，SC所成角为60°
练习册系列答案
相关题目
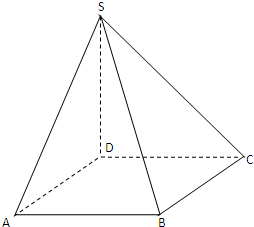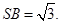
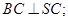
如图，SD垂直于正方形ABCD所在的平面，
如图，SD垂直于正方形ABCD所在的平面，
．
．
．
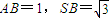