题目内容
已知函数 ,若存在
,若存在 ,使得
,使得 ,则
,则 的取值范围为( )
的取值范围为( )
A. | B. | C. | D. |
C
解析试题分析:由已知得,当 时,
时, ;当
;当 时,
时, .因为存在
.因为存在 ,使得
,使得 ,所以使得
,所以使得 的
的 ,那么
,那么 ,所以设
,所以设 ,
,
则 ,在
,在 上是单调递增的,
上是单调递增的,
设 ,则
,则 ,
, ,所以
,所以 的取值范围为
的取值范围为 .
.
考点:1.分段函数的图像与性质;2.二次函数的单调性与最值

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
函数 的零点所在的区间为( )
的零点所在的区间为( )
| A.(1,2) | B.(2,3) | C.(3,4) | D.(4,5) |
已知 ,
, ,
, ,则
,则 三者的大小关系是
三者的大小关系是
A. | B. | C. | D. |
函数f(x)=lnx的图象与函数g(x)=x2-4x+4的图象的交点个数为( )
| A.0 | B.1 | C.2 | D.3 |
若函数 的图像上存在点
的图像上存在点 ,满足约束条件
,满足约束条件 ,则实数
,则实数 的最大值为( )
的最大值为( )
A. | B. | C. | D. |
已知 是
是 上的单调递增函数,则实数
上的单调递增函数,则实数 的取值范围为 ( )
的取值范围为 ( )
| A.(1,+∞) | B.[4,8) | C.(4,8) | D.(1,8) |
函数 的单调减区间为( )
的单调减区间为( )
A.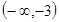 | B. | C. | D. |
若关于x的不等式 在区间
在区间 内有解,则实数a的取值范围是( )
内有解,则实数a的取值范围是( )
A. | B. | C. | D. |
已知函数 的定义域为
的定义域为 为正整数),值域为[0,2],则满足条件的整数对(m,n)共有 ( )
为正整数),值域为[0,2],则满足条件的整数对(m,n)共有 ( )
| A.1个 | B.7个 | C.8个 | D.16个 |