题目内容
在数列 中,
中,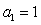 ,且对任意的
,且对任意的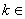
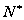 ,
,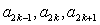 成等比数列,其公比为
成等比数列,其公比为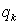 .
.
(1)若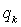 = 2(
= 2(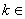
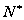 ),求
),求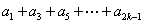 ;
;
(2)若对任意的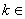
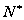 ,
,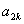 ,
,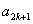 ,
,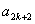 成等差数列,其公差为
成等差数列,其公差为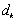 ,设
,设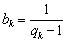 .
.
① 求证: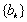 成等差数列,并指出其公差;
成等差数列,并指出其公差;
②若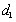 =2,试求数列
=2,试求数列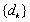 的前
的前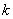 项的和
项的和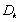 .
.
解:(1)因为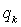 = 2,所以
= 2,所以 ,故
,故 是首项为1,公比为4的等比数列,所以
是首项为1,公比为4的等比数列,所以 , ……………………4分
, ……………………4分
(2)①因为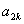 ,
,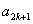 ,
,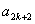 成等差数列,所以2
成等差数列,所以2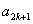 =
=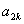 +
+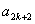 ,
,
而 ,所以
,所以 ,即
,即 ,……7分
,……7分
得 ,即
,即 ,所以
,所以 ,
,
所以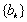 成等差数列,且公差为1. ……………………………………9分
成等差数列,且公差为1. ……………………………………9分
②因为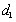 =2,所以,则由
=2,所以,则由 ,解得
,解得 或
或 ,…………10分
,…………10分
当 时,q1= 2,所以b1=1,则bk =1+(k—1)= k,即
时,q1= 2,所以b1=1,则bk =1+(k—1)= k,即 ,得
,得 ,
,
所以 ,
,
则 ,……12分
,……12分
则 ,
,
所以 ,故
,故 ,……………………………14分
,……………………………14分
当 时,q1= -1,所以b1=
时,q1= -1,所以b1= ,则bk =
,则bk = +(k—1)= k
+(k—1)= k ,即
,即 ,
,
得 ,所以
,所以 ,
,
则 ,
,
所以 ,
,
则 ,故
,故 ,
,
综上所述, 或
或 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某高校在2015年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如右图所示.
| 组号 | 分组 | 频数 | 频率 |
| 第1组 |
| 5 | 0.050 |
| 第2组 |
| ① | 0.350 |
| 第3组 |
| 30 | ② |
| 第4组 |
| 20 | 0.200 |
| 第5组 |
| 10 | 0.100 |
| 合计 | 100 | 1.000 |
(1)请先求出频率分布表中①、②位置相应的数据;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第 3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求第4组至少有一名学生被考官A面试的概率?





 ,向量
,向量 ,函数
,函数 .
.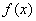 的最小正周期
的最小正周期 ;
; 分别为
分别为 内角
内角 的对边,
的对边, 为锐角,
为锐角, ,且
,且 恰是
恰是 上的最大值,求
上的最大值,求 .
. 的导数
的导数 =a(x+1)(x-a),若f(x)在x=a处取到极大值,则实数a的取值范围是 .
=a(x+1)(x-a),若f(x)在x=a处取到极大值,则实数a的取值范围是 . 中,
中, 分别为角
分别为角 的对边,
的对边, ,且
,且 .
. 的大小;
的大小; 的取值范围.
的取值范围. 的通项公式为
的通项公式为 , 则它的公差为 ( )
, 则它的公差为 ( ) D.
D. 
 ,
, 是等比数列
是等比数列 中的项,且不等式
中的项,且不等式 的解集是
的解集是 ,则
,则 的值是( )
的值是( ) B.
B. C.
C. D.
D.
 的前n项和为
的前n项和为 ,且
,且 ,
, ,且数列
,且数列 的前n项和为
的前n项和为 ,求
,求 满足条件:
满足条件: ,又
,又 ,是否存在实数
,是否存在实数 ,使得数列
,使得数列 为等差数列?
为等差数列? ,求
,求 的最大值和最小值
的最大值和最小值